hemnath
Advanced Member level 3

- Joined
- Jun 24, 2012
- Messages
- 702
- Helped
- 61
- Reputation
- 120
- Reaction score
- 57
- Trophy points
- 1,308
- Location
- Chennai
- Activity points
- 6,589
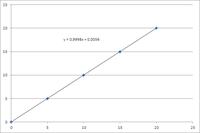
i have 5 points.
(0,0.0028), (5, 5.0056), (10, 10.0085), (15, 15.0028), (20, 20.0000)
how to find the equation for this points. what it could be the equation?
Please help.
(0,0.0028), (5, 5.0056), (10, 10.0085), (15, 15.0028), (20, 20.0000)
how to find the equation for this points. what it could be the equation?
Please help.