tipu_sultan
Member level 1

- Joined
- Jan 27, 2013
- Messages
- 41
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,296
- Activity points
- 1,626
Here find some attached circuit of three phase cabinet which operation voltage is 400V /415V and have operated current 800A, fault current for 1 sec is 46 KA and have incoming and outgoing links with one phase Lighting and socket.
I want to know is there some method that one can calculate the short circuit current per second that the bus-bar can bear.
Moreover I also want to calculate the short circuit current for 3 second.
Is there any relation between the current and time in this case (directly, or Inversely Proportion) ?
Please provide me the formula if exist to calculate short circuit current (fault-current) in any time.
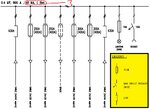
I want to know is there some method that one can calculate the short circuit current per second that the bus-bar can bear.
Moreover I also want to calculate the short circuit current for 3 second.
Is there any relation between the current and time in this case (directly, or Inversely Proportion) ?
Please provide me the formula if exist to calculate short circuit current (fault-current) in any time.



