bittersweetsep
Newbie level 4

- Joined
- Nov 28, 2012
- Messages
- 7
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,281
- Activity points
- 1,350
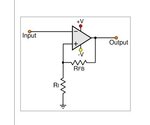
This is an inverting Schimitt trigger circuit
The op-amp is comparator here, since it is a positive feedback.
Obviously, the result is when input is higher than ground, then output goes to negative supply, while input is lower than ground, output switches to positive supply.
But my question is since the comparator is one kind of op-amp, then Vin/R1=Vout/R1+Rfb (am I right?) then how to use this equation to explain the above result???
Thanks in advance!!!

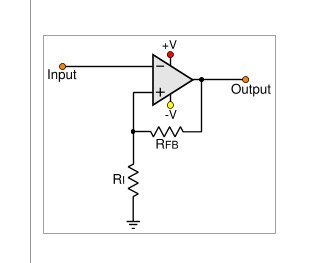
The op-amp is comparator here, since it is a positive feedback.
Obviously, the result is when input is higher than ground, then output goes to negative supply, while input is lower than ground, output switches to positive supply.
But my question is since the comparator is one kind of op-amp, then Vin/R1=Vout/R1+Rfb (am I right?) then how to use this equation to explain the above result???
Thanks in advance!!!