[SOLVED] active inductor and cap are in parallel, i can't get it resonated in desired freq?

[orz]

anyone can help me? Thx!
my active inductor's impedance in 2GHz is 1.103+j*463.194, so you can replace this circuit with a resistance and inductance in series. and the res is 1.103 Ohm with the inductance of 36.86nH.
now i put a cap(6.7809pF) on the input port like this:


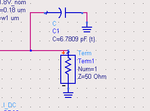
the value of cap is calculated according to the rule below:
the admittance of my circuit is Y=jwc+1/(jwL+R), so if i want it to resonate in 2GHz, the imaginary part should be zero.
(note: because the impedance of active inductor changes vs freq, a choose the resonant freq in 2GHz.)

however , the imaginary part isn't zero in 2GHz, Why? please help! Thank you!

 

[D.A.(Tony)Stewart]

What are your design layout factors, distributed capacitance and inductance and Q of filter, source impedance etc. It appears to be very low Q impedance ratio with 50 Ohms

 

[WimRFP]

Your inductor Q factor is very high, so when converting Z to a parallel equivalent circuit (Y), the inductance virtually remains 36.8 nH (with about 200kOhm parallel resistance).

To get this inductor in resonance at 2 GHz you need about 0.172 pF in parallel at the position where you "measured" the inductor impedance as stated in you posting. I just used omega^2 = 1/(LC).

I assume that you know that actually measuring the impedance curve of such a circuit in a 50 Ohms referenced system is virtually impossible.

 

[orz]

Thanks!
I don't know why 50ohm isn't suitable, would you please explain it?

 

[WimRFP]

If you would measure such a circuit with a network analyzer, the reflection coefficien is soooo high that it will be on the edge of the Smith Chart, close to RC=+1.

You may know that converting reflection coefficient back to impedance has 1/(1-RC) in the formula. When RC = 0.999 (as in your case, a very small relative change in RC will lead to a large relative change in 1-RC.

 

[orz]

Your inductor Q factor is very high, so when converting Z to a parallel equivalent circuit (Y), the inductance virtually remains 36.8 nH (with about 200kOhm parallel resistance).

yes, but why is 200kOhm in parallel? shouldn't it be 1.103 in series ?

To get this inductor in resonance at 2 GHz you need about 0.172 pF in parallel at the position where you "measured" the inductor impedance as stated in you posting. I just used omega^2 = 1/(LC).

thx! your calculation is right !
but i still don't understand , i calculate in this way :
Y=jwc+1/(jwL+R) , where R is 1.103 Ohm , so C=L/(w^2*L^2+R^2).
what is wrong?

If you would measure such a circuit with a network analyzer, the reflection coefficien is soooo high that it will be on the edge of the Smith Chart, close to RC=+1.

You may know that converting reflection coefficient back to impedance has 1/(1-RC) in the formula. When RC = 0.999 (as in your case, a very small relative change in RC will lead to a large relative change in 1-RC.

your are right, the reflection is very high. but what does "RC" mean?
i didn't get 1/(1-RC) in my formula, how did you get it? I don't really understand it .

Thanks for your help! WimRFP!

 

[WimRFP]

Sorry for not explaining. RC = reflection coefficient (S11)

Your impedance is given in a series circuit: 1.1 + j463, that means the Q factor of the inductor 421.

Now we will convert this to a parallel equivalent circuit as your capacitor is in parallel. I your capacitor was in series, you didn't need the conversion to a parallel equivalent circuit. I show you the steps how it can be done:

convert to polar notation:
|Z| = 463 Ohms (use Pythagoras) and Arg(Z) = 89.864 degrees { invtan( Im(Z)/Re(Z) ) }.

As your capacitor is in parallel, it is handy to convert your circuit to a parallel equivalent circuit (as you can add Y values for parallel ciruits).

For conversion from Z to Y:
|Y| = 1/|Z| Arg(Y) = -arg(Z): |Y| = 2.160e-3 S, arg(Y) = -89.863 degrees.

Re(Y) = 2.160e-3*cos(-89.863) = 5.13E-6 S, Im(Y) = 2.160e-3*sin(-89.863) = -2.1560e-3 S

The real part of Y is a resistor of 1/5.13e-6 = 195 kOhms
The imaginairy part of Y is an inductor of 36.84 nH (that is your high-Q inductor).

To counteract the imaginary part of -2.1560e-3 S (to get a fully real Y), you need to add +2.156e-3 S in parallel.
To do that you need a capacitor in parallel with |Z| = 1/2.156m = 463.8 Ohm -> 0.172 pF (at 2 GHz).

So at your resonant frequency, you circuit behaves as a real impedance of 195 kOhms.

If you don't like the polar conversion you may say Y = 1/(1.1+j463) and multiply this with (1.1-j463)/(1.1-j463).

If you have a low Q inductor, you will see that after the conversion from series to parellel equivalent circuit, the inductance value for the parallel equivalent circuit will not be the same.