cippy
Newbie level 5
Hi all
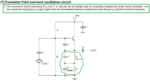
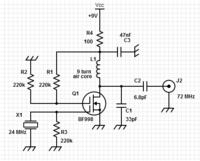
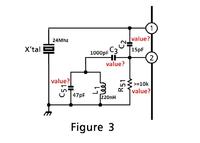
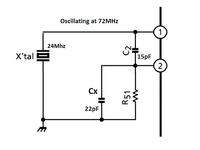
I would like someone to explain to me how I can make the circuit below work on the third harmonic.
What values do I need to C3 and C4, and how is it calculated?
desired frequency = 72 Mhz
Xtal = 24 Mhz
L2 = 220 nH
Thank in advance
Robert
I would like someone to explain to me how I can make the circuit below work on the third harmonic.
What values do I need to C3 and C4, and how is it calculated?
desired frequency = 72 Mhz
Xtal = 24 Mhz
L2 = 220 nH
Thank in advance
Robert
Attachments
Last edited: