transforming phase slope into delay

[yefj]

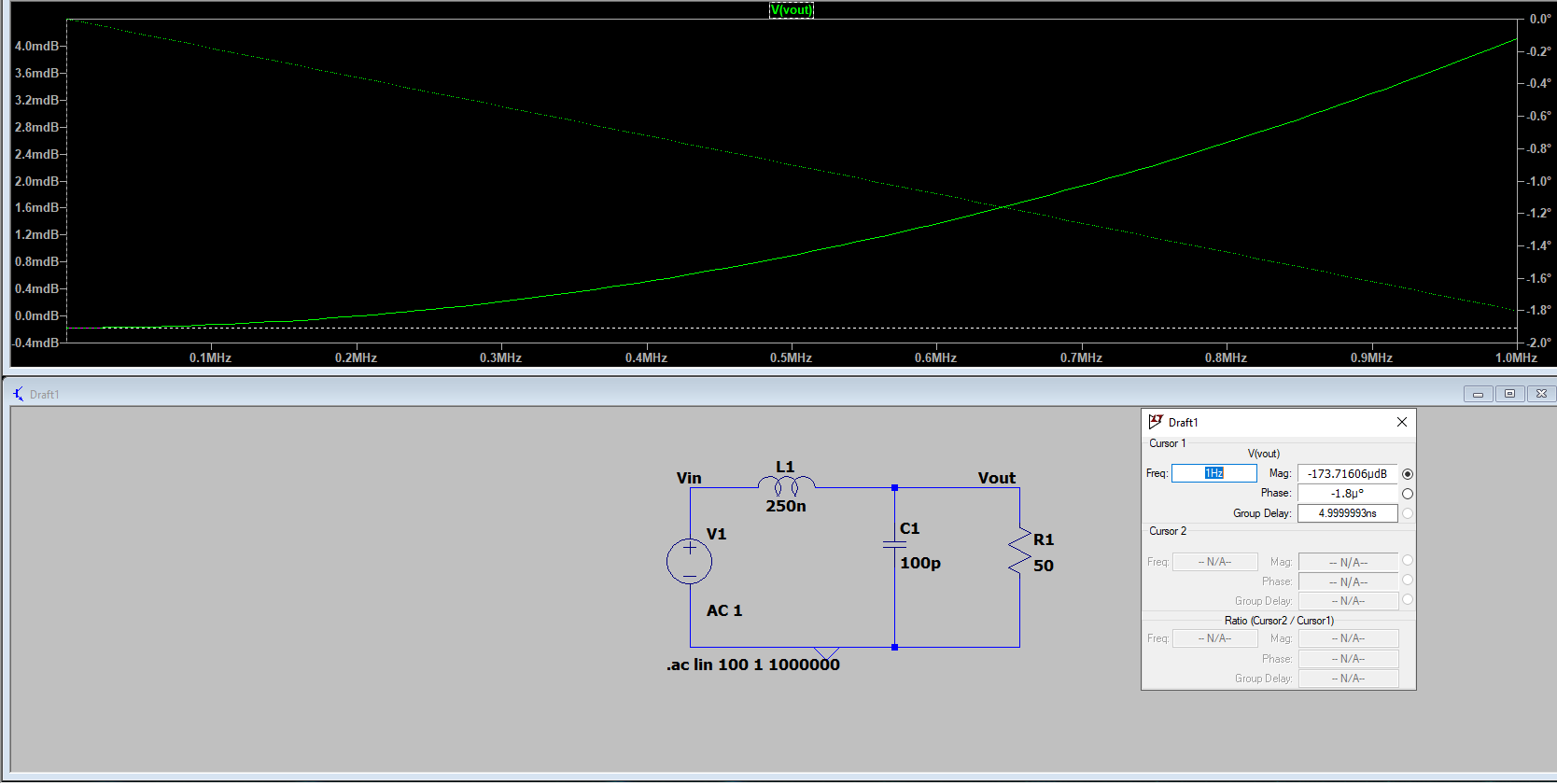
Hello, a single LC cell was made to test delay.the phase increases linearly.how do i find the delay my square wave will get from this slope?
my slope is 1.8 degrees for each 1Mhz.
Thanks.

ran

 

[danadakk]

This has a discussion of group delay in it, attached.


Regards, Dana.

 

[yefj]

Hello Dana ,by the definition of group delay
group-delay=1.8degree/1MHz=1.8Mega degrees*seconds

so if I put a pulse threw it, how do I know the time my pulse will be shifted , because the units are degrees*time

 

[danadakk]

Yes in group delay each sine component of the pulse is delayed according
to its frequency, the delay in radians. So you know the fundamental freq,
its period, is 2 * pi radians, and its harmonics as well.

From the prior ref post :

Delta t can be calced from freg and phase shift in radians.

Regards, Dana.

 

[yefj]

Hello Dana , so my LC has 38Mhz bandwidth. Suppose i want to enter a pulse with rise/fall time of 100ns.
Which means the BW of the pulse is 3.5Mhz.
I have simulated the pulse below and i got a delay of 5ns.
Given this example
How do i calculate this 5ns delay from the group delay of group-delay=1.8degree/1MHz

 

[BradtheRad]

This filter arrangement turns any repeating waveform into a sine (or sine-like). It presents a certain impedance for any given frequency. The resulting impedance is the sum of L impedance and C impedance. And somehow we can contribute the effect of R1 which has its ohm value.

The result across R1 is attenuated amplitude. The percentage of attenuation is related to the sine (or cosine) of incoming amplitude. Or it could be initial sine-shaped component of incoming waveform.

--- Updated May 11, 2024 ---

Hmmm... I'm finding the above is merely a rough idea of the theory.
Near resonance the delay is 90 degrees yet there's no attenuation .
At 3 or 4 times resonant freq the delay reaches maximum attenuation and 180 degree delay.

 

[danadakk]

Your pulse fundamental is 3.5 Mhz or 286 nS.

dT = phase (radians) / [ 2 x pi x freq *(cyc/sec) ]

What is your phase measurement at 3.5 mhz ?

Note is your source generator Z 50 ohms as well ?


Regards, Dana.

 

[yefj]

Hello Dana,regarding your assistance:
1.At 3.5MHz its -6.25.How it helps us get the pulse delay?
2.Actually its only an example.My pulse source is 74ABT04 which produses the pulse and the load is ucc5304.
How do you reccomend the source and load of the delay line given these data sheets.

https://www.mouser.co.il/datasheet/2/916/74ABT04-1541721.pdf

https://www.ti.com/lit/ds/symlink/ucc5304.pdf?ts=1715329802200&ref_url=https%253A%252F%252Fwww.mouser.co.il%252F

 

[danadakk]

You have 6 degrees of phase lag = ~ .1 radian

dT = phase (radians) / [ 2 x pi x freq *(cyc/sec) ]

dT = .1 / (2 x pi x 3.5 Mhz) = 4.5 nS

Which is in rough sim agreement with transient delay sim.


Regards, Dana.

 

[yefj]

Hello Dana , my pulse has rise time/fall time is 100ns
Ton=700ns and period is 2u.
In simple 50% duty cycle its f=1/period.But here is a more complex case.
How did you find its fundamental?
Thanks.

 

[danadakk]

I used your 3.5 Mhz as pulse period. Which is fundamental sine, then there
are 3 x 5 x 7 x......harmonics in it....

I used your 100 nS as Tr and Tf.

Regards, Dana.