juvan
Newbie level 5

- Joined
- Feb 15, 2011
- Messages
- 8
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,281
- Activity points
- 1,347
Hello, I am stuck with a problem, trying to numerically simulate, with a Method of Moments (potential of a single layer (whatever that is exactly)), the situation where I have 2 charged conductive disks, with a conductive ball in the middle. If i tried explaining the whole problem with words, it would be cumbersome, so I therefore created a picture trying to describe the problem. The information I have is the voltage on the disks ±V/2, and of course the geometry. So I guess the first issue I have to tackle, is determining the surface charge density on the disk from the voltage there, getting an integral equation something like equation (1) in the picture, then setting up the matrix equation A*σ=B and solving for σ, but the main problem I'm having is with the geometry and setting up A. I have a feeling that there is some symmetry to take advantage of, but I'm just not seeing it (note: the over all problem has symmetry in φ coordinate). To sum it all up, how do i set up the calculation for a numerical solution for a surface charge density of a charged disk.
For the sake of not writing a novel here, I will stop, and ask that if I have made anything unclear just say so and I will try to explain further.
Thanks.

- - - Updated - - -
I'm thinking of dividing the disk like this. See image. But I still have a hunch that it should be obtainable more easily, since the rings all have the same sigma. I'm thinking it could be similar to the charge distribution of a charged line, now twist that distribution 360 degrees and viola , maybe not.
, maybe not.
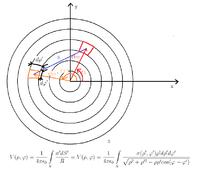
For the sake of not writing a novel here, I will stop, and ask that if I have made anything unclear just say so and I will try to explain further.
Thanks.

- - - Updated - - -
I'm thinking of dividing the disk like this. See image. But I still have a hunch that it should be obtainable more easily, since the rings all have the same sigma. I'm thinking it could be similar to the charge distribution of a charged line, now twist that distribution 360 degrees and viola
