akbarza
Full Member level 2
hi
I before posted the thread :https://www.edaboard.com/threads/why-this-circuit-oscillate.399457/ and the new my question is about it but I do not know that I must post this question in tail of it or I must open a new thread. So I decided to open a new post.
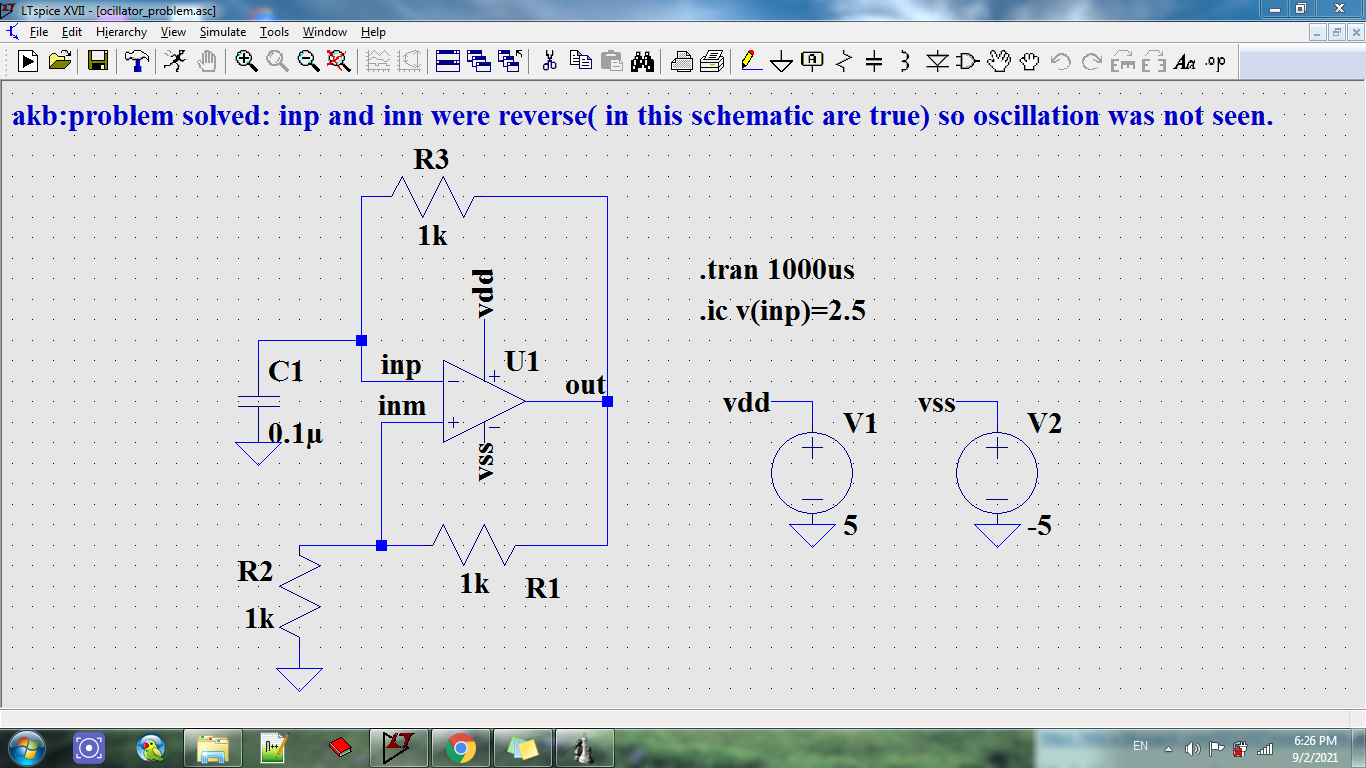
In the pic, if we replace the ideal opamp with a opamp with one pole as Ainf/(1+f/f0), how can we explain this circuit oscillation? what is the effect of f0 frequency on oscillation frequency of ideal opamp namely f_osc=1/(r3*c1*ln3)?
I tried to solve this with replacing opamp with a voltage dependent voltage source as Ainf(v+ -v-) that was serried by an r and c. but I am not sure and I do not know how solve it.
is there any explanation or guide?
in second stage, if Ainf is large but finite, what is result and effect of this assumption?
Is there any suggestion to simulate this circuit with ltspice?
THANKS
I before posted the thread :https://www.edaboard.com/threads/why-this-circuit-oscillate.399457/ and the new my question is about it but I do not know that I must post this question in tail of it or I must open a new thread. So I decided to open a new post.
In the pic, if we replace the ideal opamp with a opamp with one pole as Ainf/(1+f/f0), how can we explain this circuit oscillation? what is the effect of f0 frequency on oscillation frequency of ideal opamp namely f_osc=1/(r3*c1*ln3)?
I tried to solve this with replacing opamp with a voltage dependent voltage source as Ainf(v+ -v-) that was serried by an r and c. but I am not sure and I do not know how solve it.
is there any explanation or guide?
in second stage, if Ainf is large but finite, what is result and effect of this assumption?
Is there any suggestion to simulate this circuit with ltspice?
THANKS