Producing the sinc roll off of a DAC

[jayo57]

Producing sinc roll off of a DAC

Hi,

I'm trying to investigate a basic DDS system through the mathematical modelling of it’s operation. A generalized DDS architecture is depicted in the image below.



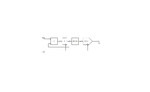
note that the DDS architecture has the following attributes:
• An accumulator comprising a binary adder and a common or garden synchronous latch.
• A phase to frequency converter, realized as a look-up table through a ROM device.
•A digital to analogue converter.

Strictly, the DAC should be followed by a reconstruction analogue filter, but I'm trying to produce the lower image frequency (a sin(x)/x response or sinc roll off) and in order to do this I need to design a mathematical model of the generalized DDS architecture using scilab/matlab for a candidate frequency setting word, and carry out a frequency analysis of the output using a fast fourier transform.

Basically I'm trying to produce the amplitude response(red) in the following image:



Any pointers on how to do this would be much appreciated.

I have managed to plot the sinc roll off in scilab using the following equation:

A(fo) = sin(π*fo/fc)/(π*fo/fc)

Where fo is the output frequency and fc is the clock frequency

The code is as follows:

Fc=100;
Roll = [sin(%pi/Fc)/(%pi/Fc),sin(10*%pi/Fc)/(10*%pi/Fc),sin(20*%pi/Fc)/(20*%pi/Fc),sin(30*%pi/Fc)/(30*%pi/Fc),sin(40*%pi/Fc)/(40*%pi/Fc),sin(50*%pi/Fc)/(50*%pi/Fc),sin(60*%pi/Fc)/(60*%pi/Fc),sin(70*%pi/Fc)/(70*%pi/Fc),sin(80*%pi/Fc)/(80*%pi/Fc),sin(90*%pi/Fc)/(90*%pi/Fc),sin(100*%pi/Fc)/(100*%pi/Fc)]; etc.......

plot(Roll);
xlabel('Time index n'); ylabel('Amplitude');
title('Sinc Roll Off');

rect=[1 -0.3 55 1.1];
zoom_rect(rect)

I have also managed to plot it in the following way;

stacksize('max')
FS=192000;
fout=1920;
t=0:1:FS;
sig=sinc(2*%pi*t*fout/FS);
//playsnd(sig,FS)
plot2d(sig)
//plot(sig)
rect=[0 -0.4 2000 1.3];
zoom_rect(rect)


Thanks in advance.