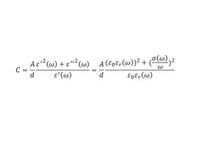Monady
Advanced Member level 4
Hi dear all friends,
I wanna find value of a capacitor made of two series materials between cap plates. These materials which are used between cap plates have both electrical conductivity and relative permittivity. Since these materials between cap plates have conductivity too, I have no ideal how I can model this capacitor and find its value. I would appreciate it if anybody give me some help.
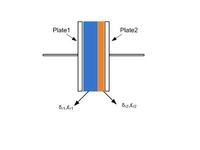
I wanna find value of a capacitor made of two series materials between cap plates. These materials which are used between cap plates have both electrical conductivity and relative permittivity. Since these materials between cap plates have conductivity too, I have no ideal how I can model this capacitor and find its value. I would appreciate it if anybody give me some help.