denizduran
Member level 2
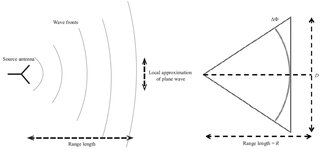
There is a 24.25 GHz Reflector design that needs to be tested. When calculating the radiation zones of the reflector, do we calculate far-field = 4 * Raleigh zone? And if so, why is the calculation in terms of the Raleigh zone and there is no mention of the Fresnel and Fraunhofer regions?