Mad-Scientist_In-Training
Newbie level 4
Hi;
I am going to build a coffee cup warmer plate using resistors - as an experiment.
Instead of using a USB port from my computer I am going to use a 5V, 700mA cell phone charger.
Using Ohms Law I have calculated that I there will be 7.14\[\Omega\] of resistance so I have ordered 3 x 2.4\[\Omega\] 5W resistors (Yageo - through-hole) and also 3 x .12\[\Omega\] resistors (Yageo - through-hole) in case they are all at the bottom end of the 5% tolerance for each resistor ((3x2.4) + (3x.12) x.95) = 7.182\[\Omega\] ... just slightly larger than the 7.14\[\Omega\] required for the circuit.
I would like to try to determine ahead of time what will be the heat dissipated from the resistors so I can 1) learn how to estimate heating of circuit components, and 2) know if I will need to use a larger or smaller supply (and resistor values).
I have not done any calculus before and I am wondering if someone can assist me with a quick tutorial on how to use the ∫ (integral) symbol to calculate the heat that would be dissipated from resistors.
I have this forumla W= ∫ V(t) I(t) dt ... with a t2 at the top of the ∫ symbol and a t1 at the bottom of the ∫ symbol.
Here's an image of the formula:
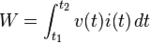
The values that I am using are:
5V,
.7A,
7.14\[\Omega\]
100% duty cycle - always on.
Thanks for any assistance.
EDIT: For clarification, I would like to try to determine the temperature that the resistors will achieve.
I am going to build a coffee cup warmer plate using resistors - as an experiment.
Instead of using a USB port from my computer I am going to use a 5V, 700mA cell phone charger.
Using Ohms Law I have calculated that I there will be 7.14\[\Omega\] of resistance so I have ordered 3 x 2.4\[\Omega\] 5W resistors (Yageo - through-hole) and also 3 x .12\[\Omega\] resistors (Yageo - through-hole) in case they are all at the bottom end of the 5% tolerance for each resistor ((3x2.4) + (3x.12) x.95) = 7.182\[\Omega\] ... just slightly larger than the 7.14\[\Omega\] required for the circuit.
I would like to try to determine ahead of time what will be the heat dissipated from the resistors so I can 1) learn how to estimate heating of circuit components, and 2) know if I will need to use a larger or smaller supply (and resistor values).
I have not done any calculus before and I am wondering if someone can assist me with a quick tutorial on how to use the ∫ (integral) symbol to calculate the heat that would be dissipated from resistors.
I have this forumla W= ∫ V(t) I(t) dt ... with a t2 at the top of the ∫ symbol and a t1 at the bottom of the ∫ symbol.
Here's an image of the formula:
The values that I am using are:
5V,
.7A,
7.14\[\Omega\]
100% duty cycle - always on.
Thanks for any assistance.
EDIT: For clarification, I would like to try to determine the temperature that the resistors will achieve.
Last edited: