Ibtissam Aziz
Newbie level 4

- Joined
- Jan 17, 2015
- Messages
- 6
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1
- Activity points
- 61
Hello,
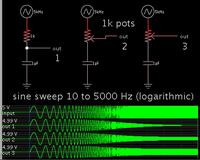
I studied filter design, I know usual canonical forms to express 1st and 2nd order filter.
These forms lead us to -20/-40dB per decade. I was wondering how to design filters that aren't -20/-40..etc dB/dec.
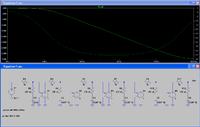
Is there other mathematical tools to do it ? I found schematics and tryed to compute transfert function and I couldn't make the identification to canonical form.
Thanks for any help :smile:
I studied filter design, I know usual canonical forms to express 1st and 2nd order filter.
These forms lead us to -20/-40dB per decade. I was wondering how to design filters that aren't -20/-40..etc dB/dec.
Is there other mathematical tools to do it ? I found schematics and tryed to compute transfert function and I couldn't make the identification to canonical form.
Thanks for any help :smile: