Saad Muftah
Junior Member level 1

- Joined
- Oct 10, 2013
- Messages
- 15
- Helped
- 1
- Reputation
- 2
- Reaction score
- 1
- Trophy points
- 3
- Activity points
- 107
Hi
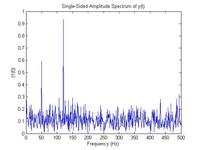
i am trying to write code to calculate 2nd harmonic from noisy signal, and i am getting stuck. Can any one help me in that.
Many Thanks,
i am trying to write code to calculate 2nd harmonic from noisy signal, and i am getting stuck. Can any one help me in that.
Many Thanks,