yefj
Advanced Member level 4
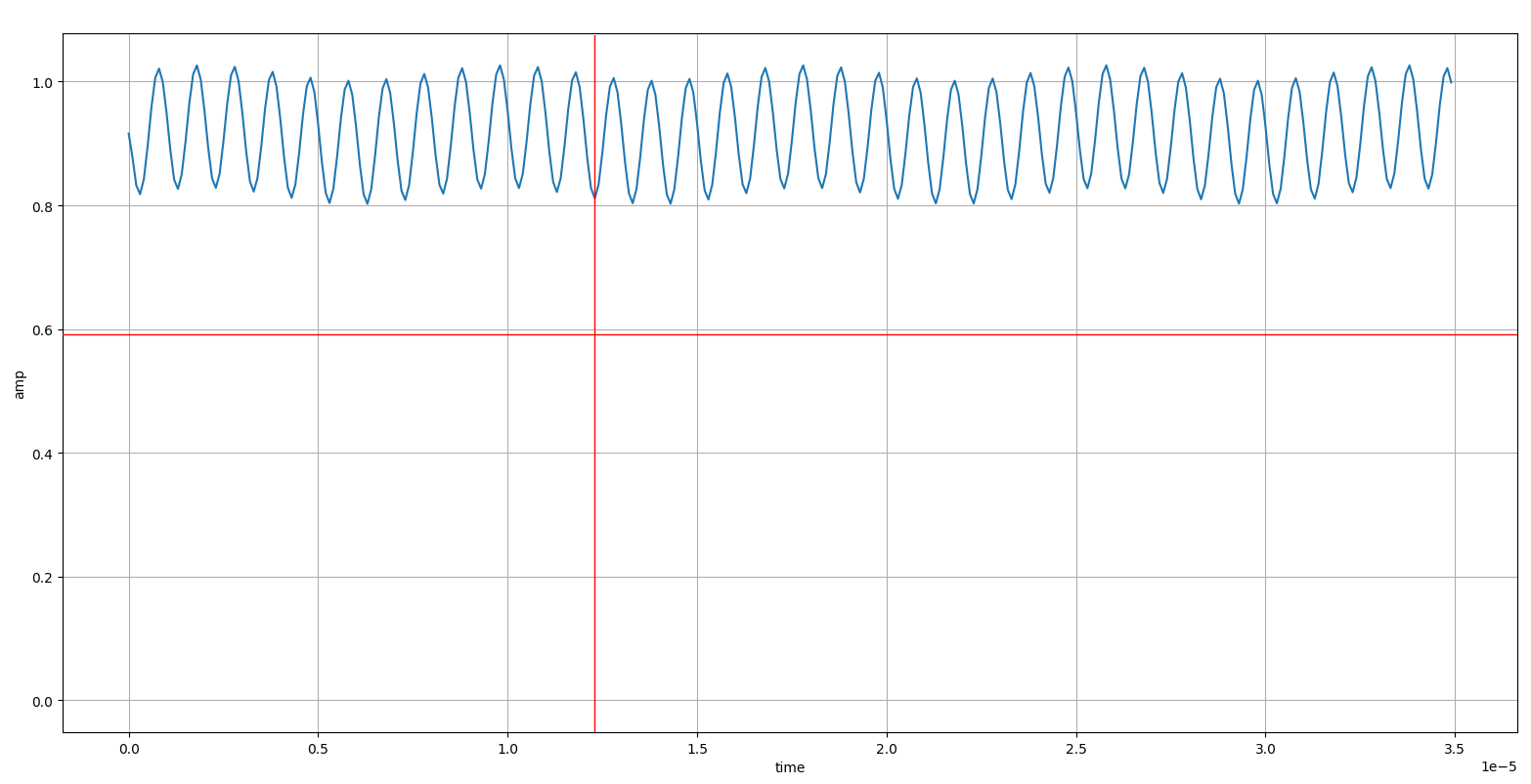
Hello, i have a signal 3.5*10^-5 sec long as shown bellow.
It was unevenly sampled so i did cubic spine interpolation.
my signal as shown in time domain about 0.9V and 1Mhz frequency.
I want to create an accurate fft picture with Fs=10Mhz So Ts=10^-7 sec
N=signal 3.5*10^-5/10^-7=350
I want an accurate FFT with 1Hz bin 350 samples is too little.(spectral leakage)
what could be done to perform a good fft in this case?
Thanks.
It was unevenly sampled so i did cubic spine interpolation.
my signal as shown in time domain about 0.9V and 1Mhz frequency.
I want to create an accurate fft picture with Fs=10Mhz So Ts=10^-7 sec
N=signal 3.5*10^-5/10^-7=350
I want an accurate FFT with 1Hz bin 350 samples is too little.(spectral leakage)
what could be done to perform a good fft in this case?
Thanks.
Code:
from scipy.fftpack import fft
#import plotly
#import chart_studio.plotly as py
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.widgets import Cursor
from gekko import GEKKO
#%matplotlib qt
new_x=np.arange(0,3.5e-05,1/(1e7))
dataset_fft=pd.read_table("sinus_1mhz.txt")
array_fft=dataset_fft.values
m=GEKKO()
m.x=m.Param(new_x)
m.y=m.Var()
m.cspline(m.x,m.y,array_fft[:,0],array_fft[:,1])
m.options.IMODE=2
m.solve(disp=False)
fig=plt.figure()
ax=fig.subplots()
ax.grid()
cursor=Cursor(ax, horizOn=True,vertOn=True,useblit=True,color='r',linewidth =1)
#plt.plot(array_fft[:,0],array_fft[:,1])
plt.plot(m.x,m.y)
plt.xlabel("time")
plt.ylabel("amp")
plt.show()
