d123
Advanced Member level 5
Hi,
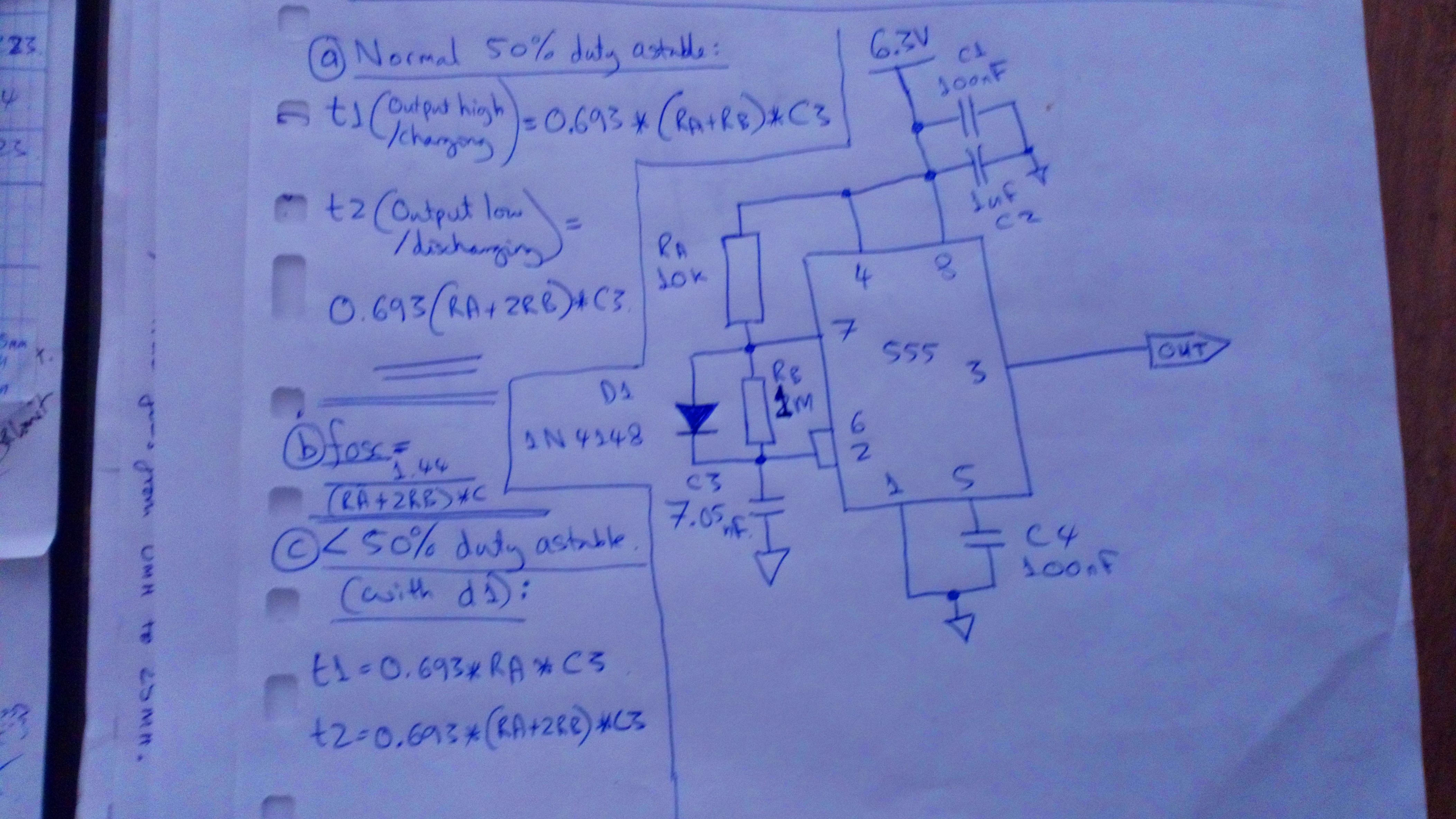
I did some calculations that were wrong, I believe, and I've just looked at a few webs and none so far show an accurate way of calculating t1 (output high, charging) for the 555 when the duty cycle is modified for <50% with a diode. They omit the diode resistance or how it affects the standard astable calculation for high output. Normal astable and astable with diode formulas are in the attached schematic/jpg.
Ra = 10k
Rb = 1M
C = 7.05nF
t1 = 0.693*10k*7.05nF = 488uS Wrong.
t2 = 0.693*(2M + 10k)*7.05nF = 9.82mS Right.
If I make t1 = 0.693*20k*7.05nF = 97.7uS Right.
Frequency counter gave 101Hz in a real circuit, and:
1.44/((10k + 2M)*7.05nF) = 100.8Hz Right/matches real circuit.
I checked 1n4148 resistance at 630uA (6.3V/10k) on a website, and it is far from 20k, it's about 100R, and doing a parallel calculation for 100R and 1M is not 20k. Not sure what I'm getting wrong.
Any ideas of how to factor in the diode resistance to the formula for t1, or how to make calculations match reality? Or point out what I have got wrong in my calculation for t1 with the 10k?
Thanks.
I did some calculations that were wrong, I believe, and I've just looked at a few webs and none so far show an accurate way of calculating t1 (output high, charging) for the 555 when the duty cycle is modified for <50% with a diode. They omit the diode resistance or how it affects the standard astable calculation for high output. Normal astable and astable with diode formulas are in the attached schematic/jpg.
Ra = 10k
Rb = 1M
C = 7.05nF
t1 = 0.693*10k*7.05nF = 488uS Wrong.
t2 = 0.693*(2M + 10k)*7.05nF = 9.82mS Right.
If I make t1 = 0.693*20k*7.05nF = 97.7uS Right.
Frequency counter gave 101Hz in a real circuit, and:
1.44/((10k + 2M)*7.05nF) = 100.8Hz Right/matches real circuit.
I checked 1n4148 resistance at 630uA (6.3V/10k) on a website, and it is far from 20k, it's about 100R, and doing a parallel calculation for 100R and 1M is not 20k. Not sure what I'm getting wrong.
Any ideas of how to factor in the diode resistance to the formula for t1, or how to make calculations match reality? Or point out what I have got wrong in my calculation for t1 with the 10k?
Thanks.