Andrew77
Member level 3
Hi all,
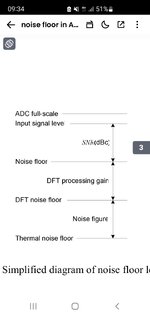
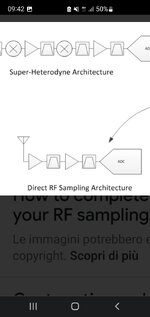
I have just a question: in a direct rf sampling receiver with a input filter from 30mhz to 500 mhz+ LNA and + ADC, what sets the bandwidth for calculation the overall thermal noise floor? Does the ADC affects the computation with its sampling rate? (Considering only the filter we can have: NoiseFloor=-174 +10log(270e6) + NFlna=-89,7+NFlna)
If I use the ADC can I decrease this value?
Thanks
I have just a question: in a direct rf sampling receiver with a input filter from 30mhz to 500 mhz+ LNA and + ADC, what sets the bandwidth for calculation the overall thermal noise floor? Does the ADC affects the computation with its sampling rate? (Considering only the filter we can have: NoiseFloor=-174 +10log(270e6) + NFlna=-89,7+NFlna)
If I use the ADC can I decrease this value?
Thanks