VT mismatch contribution of mosfets

[melkord]

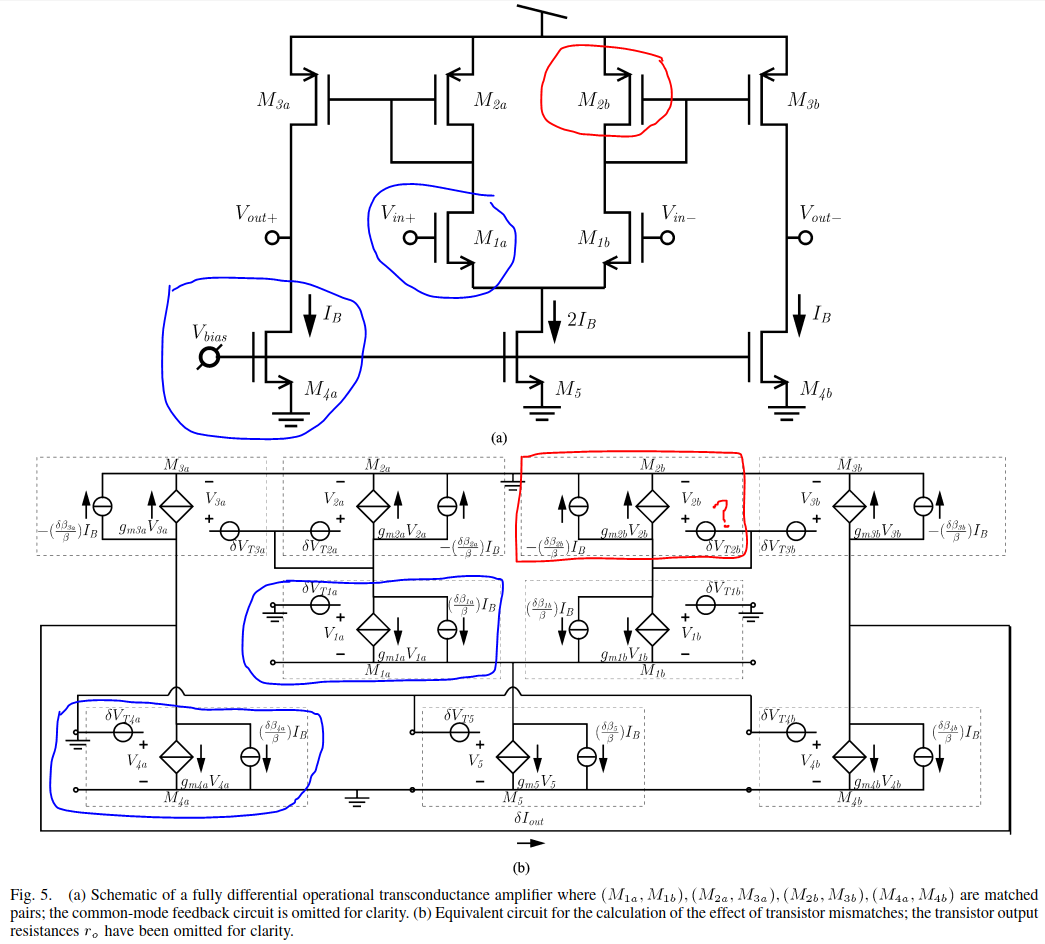
From this paper, it is shown that the input-referred offset contribution from M2b = delta_V_T2b * (gm2/gm1) , gm2=gm3.
This is done as if V2b = 0. (red mark)
But I am not comfortable with this.
Am I missing something here?

As a comparison, for other calculation, e.g., M1a and M4a, the input DC source is grounded. (blue mark).
Then, we can link it with its gm to find the output current.
This I understand.

 

[24BSNR]

You were not too clear about the specific section or equation you are asking.
I'll assume it is eq 8 p1216, you meant. In it, he explains the voffset(variance) is proportional to some weighting terms. One of which is ((gm2,3)/gm1)^2*var((deltaVT(2,3)). In order to bring this down, one can lower ratio gm2,3/gm1.

He then explains that all devices have same Id. So one needs to decrease gm2,3/I at the cost of larger deltaV and lower output swing.

I think you are questioning that comment.

If you take (gm/Id) = Beta*deltaV/(Beta*deltaV^2) = 1/deltaV
That confirms his comment.

If you are asking why the weighting factor of of the voffset contribution is gm2/gm1. I would think about it like this.

We know Iout is proportional to difference of (vgs1-vt1)- (vgs2-vt2). If vt1 and vt2 are perfectly matched it is just Iout proportional to vgs1-vgs2. For a fixed common mode this will center output difference at 0.
Now vout difference is proportional to gm1*(diff(vin))*(1/gm2). Again, a vt mismatch would offset this ideal value from 0 because diff(vin) is no longer zero. (but vt difference) So to lower this effect, one could lower ratio gm2/gm1. This brings us back to first point.