The dispersion diagram for the coplanar waveguide

[pikuha]

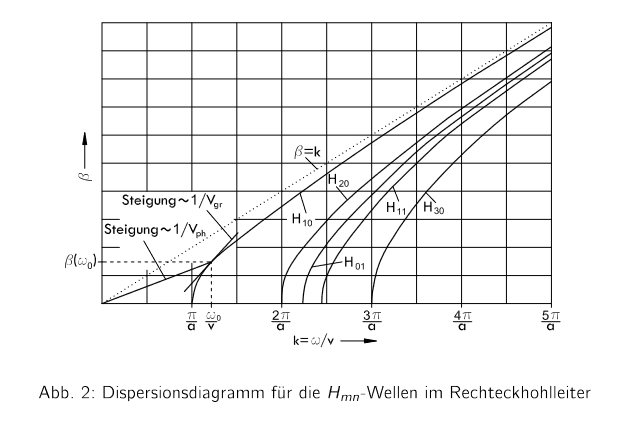
Hello everyone! My question relates to the dispersion diagram (I've attached Abb. 2).
I have a coplanar waveguide and have to plot the dispersion diagram ω(β), where ω - angular frequency and β - the phase constant.
I have found some information about the dispersion diagram for the rectangular waveguide, where the TEM mode exists. But as I know, in the coplanar waveguide exists quasi TEM mode and the coplanar waveguide isn't a rectangular waveguide, I couldn't use geometric parameters like the height b and the width a (I've attached Abb. 1) to calculate mods for the dispersion diagram.

If I would like to plot the angular frequency versus the phase constant for the coplanar waveguide, I can't just multiply ω*β, or?

So, I am not sure, how it works for the coplanar waveguide.

If you have any related information, please let me know. I'd be grateful!

 

[PlanarMetamaterials]

Welcome, pikuha.

Coplanar waveguide (assuming no conductor backing) and a rectangular waveguide are generally not relatable. For a given coplanar waveguide, I would probably choose to simulate it in an eigenmode solver to obtain the correct dispersion curves.

If I would like to plot the angular frequency versus the phase constant for the coplanar waveguide, I can't just multiply ω*β, or?

Yes, for the quasi-TEM mode. This however makes a number of approximations, such as a lack of coupling with the higher-order modes, no radiation, etc. The linear relation is only really valid for low frequencies.

You may also want to check out work by Rainee Simons; he has done extensive work with coplanar waveguides and might have investigated higher-order modes.

 

[pikuha]

Thank you so much, PlanarMetamaterials

When you say "simulate it in an eigenmode solver" do you mean such programs as HFSS?

I was wondering if an analytic formula for calculating the dispersion diagram exists. I see only plots and conclusions when I find some information about this topic and nowhere formulas or calculations.


Thank you so much for the lead about Rainee Simons. I got his book from the library

 

[PlanarMetamaterials]

When you say "simulate it in an eigenmode solver" do you mean such programs as HFSS?

Yes. Most commercial 3D EM solvers will be able to do this. I've done it extensively in HFSS.

I was wondering if an analytic formula for calculating the dispersion diagram exists. I see only plots and conclusions when I find some information about this topic and nowhere formulas or calculations.

You essentially already had it; we know that

\[ \beta = \frac{\omega}{v_p} \]​

where \(v_p\) is the phase velocity of the mode. Obtaining this phase velocity is the hard part; it will usually depend on effective permittivity \(\epsilon_{eff}\) , which you can find derived analytically in texts such as Simons'.

It's an exceedingly difficult task to analytically derive the dispersion properties of the high-order modes of a CPW; I don't know if I've ever seen a complete solution. So, we usually just extract the dispersion properties from simulation.

Thank you so much for the lead about Rainee Simons. I got his book from the library

Enjoy!