Adam12
Newbie level 3

Hello there,
I am a newbie here,
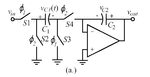
Can you experts please let me know in a Switch-Cap integrator like the one in the below pic, what thing determines the MAXIMUM clock frequency the circuit can go?
I deigned a continuous integrator with the input frequency of 600kHz (and the gain of 1), and then designed its equivalent Switch-Cap integrator... I selected the clock frequency to be at 40X (ie 24MHz)... I noticed that at 24MHz the gain is not exactly 1 for the switch cap, but it is less than that, and I noticed that the phase of the "Clock Frequency" is "93" degree! I then tried to reduced the input frequency to 100kHz and the clock to 4MHz, then I saw that the gain of the SC integrator changed to what I expected (ie 1) and the clock phase phase also changed to 90 degree... So whats wrong here? What causes the clock frequency to go to 93 degree at 24MHz?
Thank you so much or any help.
I am a newbie here,
Can you experts please let me know in a Switch-Cap integrator like the one in the below pic, what thing determines the MAXIMUM clock frequency the circuit can go?
I deigned a continuous integrator with the input frequency of 600kHz (and the gain of 1), and then designed its equivalent Switch-Cap integrator... I selected the clock frequency to be at 40X (ie 24MHz)... I noticed that at 24MHz the gain is not exactly 1 for the switch cap, but it is less than that, and I noticed that the phase of the "Clock Frequency" is "93" degree! I then tried to reduced the input frequency to 100kHz and the clock to 4MHz, then I saw that the gain of the SC integrator changed to what I expected (ie 1) and the clock phase phase also changed to 90 degree... So whats wrong here? What causes the clock frequency to go to 93 degree at 24MHz?
Thank you so much or any help.