solution to a contradiction on linear system principles (i.e LC filter)

[devilwiss]

Hello everybody.

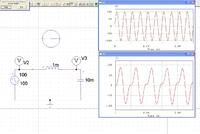
"the frequency of the output response of a linear system is the same as the freq of the input signal"

I think this statement is true but i'm no longer sure about it, since i've seen that the response of a lossless LC filter for a step input is a periodic waveform !!

Please i need a solution for this apparent contradiction.

Thanks in advance

 

[BradtheRad]

If a step input means a sudden jump in voltage/current...

Then it will instigate the LC filter to oscillate at its resonant frequency. It will 'ring'.

This is a different behavior from applying a sine wave to the LC filter.

A step input is not any particular frequency. It's more like a power-up or down jolt.

 

[FvM]

I would say, the statement is at least imprecise.

How do you describe the "frequency" of a step function?

 

[LvW]

"the frequency of the output response of a linear system is the same as the freq of the input signal"

This sentence applies only (a) if the system is under steady state conditions (not for the step response) and (b) for the FREQUENCY (but not for the amplitude of the signal).
In your case, you observe a damped oscillation as the step response of an LC circuit.

 

[FvM]

Trying to read a sense into the original statement, you can say that the output of a linear system has only frequency components that are also contained in the input signal. This is true for steady state and transient response as well. You can check by looking at the signals' laplace transformations. The step function (laplace function L(s) = a/s) contains "all" frequencies, with decreasing magnitude.

 

[devilwiss]

To be more explicit, Please let me propose this example.

Let's take the case where we put a periodic waveform in the input of the lossless LC filter.

in the output waveform we see two components ne at the freq of the input (which is obvious) and the other at the ringing freq of the filter (1/2*pi*sqrt(LC)) (valid in the transient and steady state conditions)

The lossless filter adds its ringing freq component to the output even if the input signal doesn't contain the ringing freq component !!!

This is in contradiction with the principle of a linear system !!

 

[FvM]

The assumption is wrong, there won't be any ringing in the steady-state case.

 

[devilwiss]

This is true !!

You can see the waveforms in the picture using PSIM soft.



We can see that the output waveform is distorted, the proof that it's contains many freqs (in this case 2 freq)

Best regards

 

[LvW]

Are you sure that the L model contains no non-linearities?

 

[devilwiss]

I can confirm that the inductance contains no linearities.

 

[LvW]

A lossless LC circuit does not exist in reality and, thus, never reaches steady-state conditions after being energized.
Thus, the response to a switch-on never goes to zero - and superimposes with the input signal.

 

[FvM]

A lossless LC circuit does not exist in reality and, thus, never reaches steady-state conditions after being energized.
Thus, the response to a switch-on never goes to zero - and superimposes with the input signal.

Yes, of course. In addition, the shown waveform would be far from steady state even for lossy LC filter, because it's starting at t=0.