chiques
Full Member level 3
- Joined
- Nov 21, 2007
- Messages
- 169
- Helped
- 2
- Reputation
- 4
- Reaction score
- 2
- Trophy points
- 1,298
- Location
- California
- Activity points
- 2,543
Hello Forum Peeps,
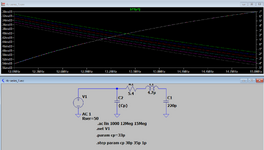
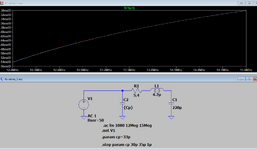
I have a series resonant circuit which I have simulated and built on an actual grounded coplanar waveguide. My question is regarding the Q factor of the circuit. In the case of the LTSpice simulation, I used generic (ideal) lumped resistor, inductor and capacitor. I added this resistor only because my signal generator has a 50 Ohm impedance (not sure if this is correct) although nonexistent on the physical circuit.

I’m trying to wrap my head around the fact that even in an ideal world, my circuit Q will only be as high as 9.1.

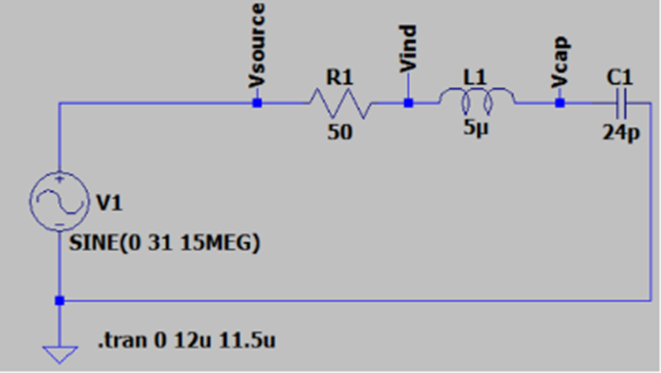
Am I using the correct R or is this more like the DCR of the inductor?
For example: CoilCrafts 1812CS-472XJR is specified to have a DCR of 5.4 Ohm and a Q of 63.
1812CS-472XJR_ 4.7 @ 7.9 MHz 5 63 @ 50 MHz 115 5.4 230
https://www.coilcraft.com/getmedia/677afbbb-f368-4f0b-b59e-ab9befcb1f0e/1812cs.pdf
What about the capacitor, won’t that affect the Q factor the circuit as well?
I’m asking this because I’m currently using a high current pulse inductor PA4548.472NLT (seen on my board) but the datasheet does not show Q. I noticed many high current inductors such as this do not have a specified Q. Is this because they are not intended to be used in RF? I'm guessing the Q is so bad they don't want to publish it..???
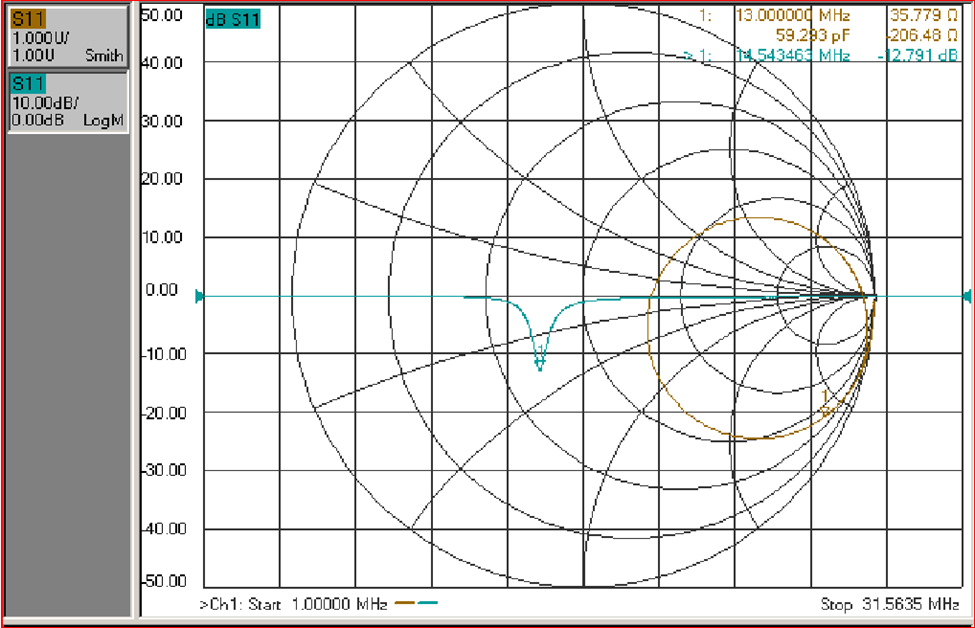
My goal is to get a better return loss than -12.8dB
I have a series resonant circuit which I have simulated and built on an actual grounded coplanar waveguide. My question is regarding the Q factor of the circuit. In the case of the LTSpice simulation, I used generic (ideal) lumped resistor, inductor and capacitor. I added this resistor only because my signal generator has a 50 Ohm impedance (not sure if this is correct) although nonexistent on the physical circuit.
I’m trying to wrap my head around the fact that even in an ideal world, my circuit Q will only be as high as 9.1.
Am I using the correct R or is this more like the DCR of the inductor?
For example: CoilCrafts 1812CS-472XJR is specified to have a DCR of 5.4 Ohm and a Q of 63.
1812CS-472XJR_ 4.7 @ 7.9 MHz 5 63 @ 50 MHz 115 5.4 230
https://www.coilcraft.com/getmedia/677afbbb-f368-4f0b-b59e-ab9befcb1f0e/1812cs.pdf
What about the capacitor, won’t that affect the Q factor the circuit as well?
I’m asking this because I’m currently using a high current pulse inductor PA4548.472NLT (seen on my board) but the datasheet does not show Q. I noticed many high current inductors such as this do not have a specified Q. Is this because they are not intended to be used in RF? I'm guessing the Q is so bad they don't want to publish it..???
My goal is to get a better return loss than -12.8dB