STINGERX
Junior Member level 3

Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.







Well you said you already know algebra and that's algebra. ;-)
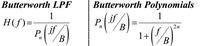


SingerX,
at first, here are some basics on Butterworth approximation:
1.) For comparison, you need the n-th order lowpass function (normalization Ω=ω/ωc, ωc=3dB cut-off):
A(jΩ)=ao/[1+d1(jΩ)+d2(jΩ)²+d2(jΩ)³+...+]
2.) The MAGNITUDE function for a Butterworth approximation (n-th order) is
A(Ω)=Ao/SQRT[1+Ω^(2n)]
3.) Now you have to find the MAGNITUDE of the first expression and perform a comparison of the coefficients (d1...dn) ) with the second expression in 2.).
(That´s a nice task!!)
4.) Find the transfer function of the CIRCUIT you have in mind and compare again the coefficients of the corresponding parts in the denominator. This gives you parts values (R, L, C).

4.) Find the transfer function of the CIRCUIT you have in mind and compare again the coefficients of the corresponding parts in the denominator. This gives you parts values (R, L, C).