Michael Craft
Newbie level 3
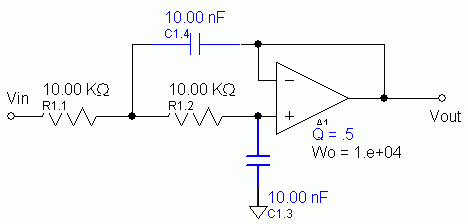
I am looking at someone's design of an active, second-order filter. Here it is:
https://i1103.photobucket.com/albums/g471/ohio_rifleman/2ndorderfilter.jpg
I find this design unusual, in that it is simply two, passive, first-order filters connected in series followed by an op amp buffer. I have never seen this before; in my experience, active, second-order filters always have a Sallen-Key or multiple feedback topology.
Why would someone use this filter in lieu of a Sallen-Key or multiple feedback topology? Are there any advantages to this design? Are there disadvantages to this design? If so, what are they?
Thank you
https://i1103.photobucket.com/albums/g471/ohio_rifleman/2ndorderfilter.jpg
I find this design unusual, in that it is simply two, passive, first-order filters connected in series followed by an op amp buffer. I have never seen this before; in my experience, active, second-order filters always have a Sallen-Key or multiple feedback topology.
Why would someone use this filter in lieu of a Sallen-Key or multiple feedback topology? Are there any advantages to this design? Are there disadvantages to this design? If so, what are they?
Thank you