Quantization error in duty cycle measurement

[kokokosini123]

Hi, I am using a counter to measure the duty cycle of a square wave, as shown in Fig(1).
Fig(1).

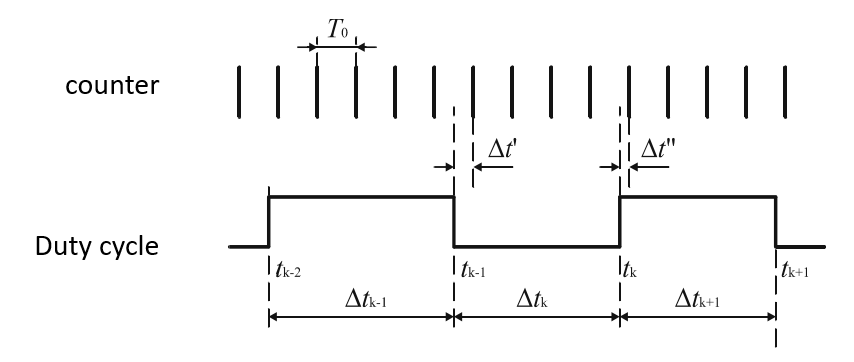
The width of the time interval Δtk can be calculated by $Δt_k=(N_k-1)T_0+Δt'+(T_0-Δt'')=N_kT_0+Δ_q\\where Δ_q=Δt'-Δt''$
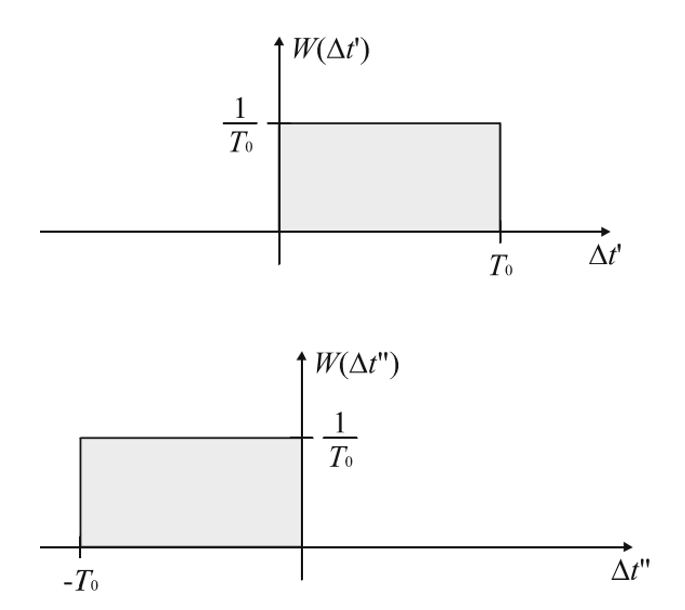
The errors Δt' and Δt'' can be considered as random variables independent of each other that range from 0 to T0 and from -T0 to 0 with PDFs shown in Fig(2). And the sum of them is the convolution of their PDF as shown in fig(3).
Fig(2).

Fig(3).

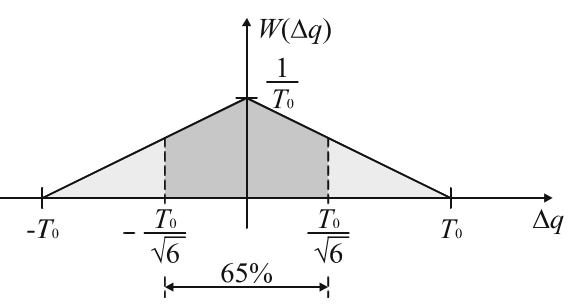
Now I need to calculate the duty ratio of the square wave which is $$\frac{Δt_k}{Δt_k+Δt_{k+1}}$$ what is the PDF of the final result?

 

[Akanimo]

Hi,
First off, what is $N_k$? Can you explain?

It seems like in your figure 1 $N_k$=4. Is that correct?

 

[kokokosini123]

Hi,
First off, what is \(N_k\)? Can you explain?

It seems like in your figure 1 \(N_k\)=4. Is that correct?

Hi,
Sorry I forgot to explain.
Yes, $N_k$ is 4.
$N_k$ means the number of counter during $Δt_k$(when the square wave is low).
The duty ratio of the square wave between $Δt_k+Δt_{k+1}$ can then be calculated by $\frac{N_k}{N_k+N_{k+1}}$
If the frequency of the counter is finite, then quantization error will appear because the counter might not land exactly on the rising/falling edge of the square wave.

 

[Akanimo]

If I am not mistaken, shouldn't the duty ratio be $\frac{Δt_{k+1}}{Δt_k+Δt_{k+1}}$?
${Δt_{k+1}}$ is the ON interval whereas ${Δt_k}$ is the OFF interval.

 

[kokokosini123]

If I am not mistaken, shouldn't the duty ratio be \(\frac{Δt_{k+1}}{Δt_k+Δt_{k+1}}\)?
\({Δt_{k+1}}\) is the ON interval whereas \({Δt_k}\) is the OFF interval.

Yes you are right, I wrote it wrongly, but I think the PDF of quantization error will not be affected.

 

[Akanimo]

I tried something. This is up for verification and so should be reviewed.

I tried to solve for the duty ratio, and this is what I got:
$\frac{Δt_{k+1}}{Δt_k+Δt_{k+1}}=\frac{N_{k+1}T_0+Δt''+Δt'''}{(N_k+N_{k+1})T_0+Δt'+Δt'''}$
where:
the error Δt''' is the time from the last count to the falling edge during $Δt_{k+1}$, necessary because we also have to consider an entire switching cycle.
$N_{k+1}$ is the number of counts during $Δt_{k+1}$.
Notice that I consider Δt''' as being separate from Δt' and Δt'' because it could be different from each of them at any instance.

If this is correct, then we have a function of three variables to be integrated. The variables are Δt', Δt'' and Δt'''.
Now, what would be their limits.

--- Updated Oct 17, 2020 ---

I think this might be helpful.

 

[kokokosini123]

I tried something. This is up for verification and so should be reviewed.

I tried to solve for the duty ratio, and this is what I got:
\(\frac{Δt_{k+1}}{Δt_k+Δt_{k+1}}=\frac{N_{k+1}T_0+Δt''+Δt'''}{(N_k+N_{k+1})T_0+Δt'+Δt'''}\)
where:
the error Δt''' is the time from the last count to the falling edge during \(Δt_{k+1}\), necessary because we also have to consider an entire switching cycle.
\(N_{k+1}\) is the number of counts during \(Δt_{k+1}\).
Notice that I consider Δt''' as being separate from Δt' and Δt'' because it could be different from each of them at any instance.

If this is correct, then we have a function of three variables to be integrated. The variables are Δt', Δt'' and Δt'''.
Now, what would be their limits.

--- Updated Oct 17, 2020 ---

I think this might be helpful.

Hi,
Many thanks, I agree with your formula, but I am not sure how will the division change the PDF, according to Fig(3) the pdf of the numerator Δt''+Δt''' is a triangular distribution and I think the denominator Δt'+Δt''' should also have the same distribution, I have searched on the internet and WIKI says the division of random variables is ratio distribution, if the two variables are independent.

And how could I know whether Δt''+Δt''' and Δt''+Δt''' are dependent or not?

 

[Akanimo]

To determine whether they are independent, we might need to make some assumptions.

Looking at a particular system, is the waveform of constant frequency? Will a certain number of counts (of the measuring counter) be always made to have exact period as the pulsating waveform? And so on.

 

[KlausST]

Hi,

You have to treat them as independent. At least I think so.

Although both two timings depend on each other, but both timings (edges) should be independent of counter clock and counter clock is non synchronous to the PWM. (Please correct me if this is not the case).

Because the timing is independent I think one can average several measurement values to get better resolution and precision.

Klaus

 

[kokokosini123]

Hi,

You have to treat them as independent. At least I think so.

Although both two timings depend on each other, but both timings (edges) should be independent of counter clock and counter clock is non synchronous to the PWM. (Please correct me if this is not the case).

Because the timing is independent I think one can average several measurement values to get better resolution and precision.

Klaus

Hi,
Thanks for your apply,

I also think they are independent, according to simulation the quantization error of the duty ratio can be reduced by average several measurement, so I think the pdf of duty ratio should have a shape with expectation at zero.

Is there any way to find the exact pdf shape of the ratio of these two independent variables?

--- Updated Oct 20, 2020 ---

To determine whether they are independent, we might need to make some assumptions.

Looking at a particular system, is the waveform of constant frequency? Will a certain number of counts (of the measuring counter) be always made to have exact period as the pulsating waveform? And so on.

Hi,

Now I treat them as independent variables, and I assume the denominator and numerator have same triangular shaped PDF, how could I find the result PDF of the ratio?

 

[Akanimo]

We can simplify things if we have a way to make $Δt'''=T_0-Δt'$. We can achieve this by making $NT_0 = one$ $PWM$ $cycle$, where N is the total number of counts in one PWM cycle. This does not mean that The PWM must be synchronous to the counts.

This will be a specific case of a possible more general case.

I'll explain exactly what I mean in my next post on this thread.