Op-amp AC characteristics measurement

[Junus2012]

Dear Friends

I finished the simulation of my op-amp design. Now I would like to know the real measurement setup for every test. Starting here in thispost with simulating the AC characteristics (Open loop gain, f-3dB, Phase Margin) .

As you know that dealing with an open loop amp is really difficult, therefore an approach like the one I attached is used for this purpose. The problem I dont understand how it working and by which equiepemnt we can scan the frequency and how we can read it to be like the one we simulate.

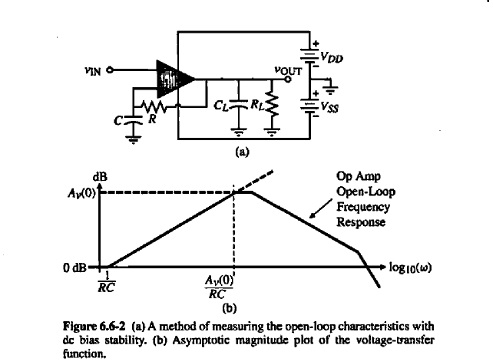
Please i really need your kind help
Regards

 

[LvW]

Hi Junus,

the shown test setup has unity gain for dc only - that is necessary to ensure an operating point within the opamp´s linear range. Otherwise, the offset voltage would bring the output into saturation because of the large open-loop dc gain.
The capacitor C should be as large as possible because - together with the large R - it creates a large time constant equivalent to a very low corner frequency wc.
Thus, for frequencies above wc the inverting input (increasingly) is ac grounded and you can measure/simulate the open-loop gain by connecting a swept frequency signal at Vin.
The load componenets (RL and CL) are not too important. Thus, some kind of normal operation conditions are established..

Remark: The rising linear curve starting at 1/RC is the inverse feedback factor 1/Hf with Hf=1/(1+sRC). Thus, the bold line is identical to the gain of the whole circuit (with feedback).
The crossing of both functions gives you the frequency w1=Av(0)/RC above which the measurement is identical to the desired open-loop gain of the opamp alone. This curve clearly shows why you should select a large time constant RC.

 

[FvM]

by which equiepemnt we can scan the frequency and how we can read it to be like the one we simulate

Signal generator, attenuator, level measurement, e.g with an oscilloscope.

 

[Junus2012]

Thank you very much LVW

your explanation is very sufficient , I think you are a teacher in this subject really

I hope to see your replies with the next measurements I would post

Thank you in advance Sir

Regards

- - - Updated - - -

Signal generator, attenuator, level measurement, e.g with an oscilloscope.

Kindly, If it is possible for you to suggest me the equipment,

Any way how could I measure the phase Margin ??

 

[LvW]

Any way how could I measure the phase Margin ??

Measure or simulate?
Or estimate? In this case, I guess the phase margin in case of unity gain feedback is only PM=5...10 deg.
(It is determined based on the corresponding phase response, which can be approximated from the gain slope at the cross-over frequency).

 

[Junus2012]

I mean measuring the phase margin, how to do that practically from the oscilloscope ?

Measure or simulate?
Or estimate? In this case, I guess the phase margin in case of unity gain feedback is only PM=5...10 deg.
(It is determined based on the corresponding phase response, which can be approximated from the gain slope at the cross-over frequency).

 

[FvM]

You don't primarly measure phase margin, you determine the phase of the open loop transfer function which allows to calculate phase margin for specific feedback factors.

The phase can be measured with an oscilloscope if you don't have special instruments for this purpose (e.g. a vector network analyzer). The input signal or a respective reference signal from the signal generator have to be connected to the oscilloscope too. Modern DSOs have suitable measurement functions to determine phase differences accurately.

 

[LvW]

I mean measuring the phase margin, how to do that practically from the oscilloscope ?

As an alternative, you can measure the step response of the closed-loop using the oscilloscope. The overshoot you can observe is a good indication of the phase margin.
There are graphics overshoot=f(phase margin), which can be used for this purpose.
This relationship normally holds for second order circuits only, but can be used with good accuracy also for third-order systems (this sufficient for opamp applications).

 

[Junus2012]

Thank you very much guys for your kind explanation, I will think more about it to ask you further

Have fun

Best Regards

 

[Junus2012]

Dear FvM and LvW

I have found this paper to calculate the phase margin from the step response overshoot , but the equation he used is not clear. Kindly, do you have any clear article regarding the same methods ??

many thanks

 

[LvW]

Junus,

I think - the equation is quite clear: PM as a function of the damping factor, which is identical to 1/2Q.
However, this requires the knowledge of Q for the closed feedback loop.
Therefore, I attach a copy from a textbook (S. Franco: Design with opamps and analog int. circuits).
There you can find a graph overshoot=f(PM).

 

[Junus2012]

Thank you very much LvW, so nice