Nodal Analysis with complex IC circuit

[lucky6969b]

**broken link removed**

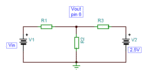
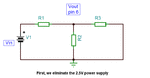
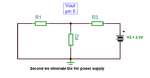
How do I use nodal analysis to analyse this kind of circuit?
Especially with the voltage level circled in the picture...
Thanks
Jack

 

[sv1437]

Nodal Analysis:
For the voltage level circled in the picture, they are treated as a single node. Let Vi: analog input; V1:voltage for the node between R1 and R2 and V2 voltage at the resistor 390 node.

(V1-Vi)/R1 +V1/R2 +(V1-V2)/R3 = 0;
(V2-5)/390 +(V2-V1)/R3 = 0;

I think 1uF capacitor is just reducing the noise across the power supply(5V), you can use the capacitor as well in your nodal analysis, but you need to know the frequency of operation, for DC you can neglect.

I hope this is what you are asking.

 

[lucky6969b]

Hi, sorry for reviving this old thread. The frequency is 1MHz
I cannot get this one V1-V2/R3, does that mean R3 is parallel to R1 and R2? is it the reason why?

Could you please elaborate?
Also in the second equation, how come we don't need to count the voltages up to the ground rail. Just from 5V to V2 / 390Ohms then V2 to V1/R3 = 0
Because there is a ground reference point across the cap?
Also how come nodel analysis is not in the direction of higher potential to lower potential. In your equation, it seems to be other way round.. correct me if I am any wrong.... you seem to be seeking every voltage from the point in question to another point having another potential. Sorry for being dumb

As well, nodal analysis seems to be easier than using the Kirchhoff voltage law...
Thanks
Jack

 

[andre_luis]

At circuit above is not clear where is nodes V1 and V2 that you refer.

+++

 

[mister_rf]

You are trying to analyze a circuit without taking in considerations all the elements there.
ZN448E = Analog to Digital converter. Pin7 = Internal reference =2.5V
So in this case R=390 ohms , C=1uF it’s not important any more. There’s a simple DC circuit as we have detailed here:
https://www.edaboard.com/threads/216209/#post916330

 

[mister_rf]

You can use the Superposition Theorem, and to eliminate all but one source of power within a network at a time, and using series/parallel analysis to determine voltage drops within the modified network for each power source separately. Then, once voltage drops (or currents) have been determined for each power source working separately, later the values are all "superimposed" on top of each other (this means added algebraically) to find the actual voltage drops with all sources active.

 

[lucky6969b]

Actually, at first blush, I am not quite sure how to do analysis on circuits such as the ones you posted in #6.
When there are 2 sources established on both sides of the diagram, how do you find the voltages/currents at various points?
I mean even when one source is eliminated, there is still a resistor on the empty side, does that resistor count?
If I remember from my college year, it is a series with 2 resistors in parallel, am i correct?
Any pointers are greatly appreciated! or web sites?
https://www.edaboard.com/threads/216627/
Thanks
Jack

 

[mister_rf]

:grin: I need some time to do all re-calculation of the circuit, better read here some technique used to mathematically analyze a circuit:
Lessons In Electric Circuits -- Volume I (DC) - Chapter 10

 

[Prof78]

Actually, at first blush, I am not quite sure how to do analysis on circuits such as the ones you posted in #6.
When there are 2 sources established on both sides of the diagram, how do you find the voltages/currents at various points?
I mean even when one source is eliminated, there is still a resistor on the empty side, does that resistor count?
If I remember from my college year, it is a series with 2 resistors in parallel, am i correct?
Any pointers are greatly appreciated! or web sites?
https://www.edaboard.com/threads/216627/
Thanks
Jack

In using the superposition theorem you do not 'eliminate' all the voltage sources bar one, you replace them with the equivalent internal impedance (resistance for this d.c. case); a voltage source has, by definition zero internal impedance (a real source will generally have some but it is generally small). A 'current source' has by definition infinite internal impedance and can therefore in effect be eliminated. Thus you do not then have open loops as concerns you. It is also most important to remember that this approach can only be used for linear circuits, not for nonlinear systems.
Prof78