[SOLVED] Need Help: Converting LDR resistance to LUX

[ArdyNT]

I need to display the LUX on the LCD by using LDR. My problem is in calibration. Actually it can be done by comparing the real LUX meter with my LDR resistance and find the factor. But I don't have LUX meter for now, so I decide to use the following graph which is provided by the datasheet:



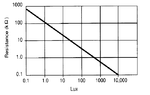
Now, can somebody help me to find the multiplication factor or maybe the equation that shows the relation between LDR resistance (y-axis) with LUX (x-axis). I really have a problem with this logarithmic graph. Help please....

 

[zorro]

Hi ArdyNT,

I[lux] = 10000 / (R[kΩ]*10)^(4/3)

Regards

Z

 

[ArdyNT]

Hi there, thank you.

Can you tell me how can you convert that logarithmic graph to that equation? Is there any reference? (I really want to understand it too)

 

[zorro]

I'll try to proceed stp-by-step.
We convert the log-log graph into a linear one by this change of variables:

x = log10(I[lux])
y = log10(R[kΩ])

Then we have the same graph but the abscissa axis is linear (ranging from -1 to 5) and the y too (ranging from -1 to 3).
It is a straight line whose equation is

(y-2)/x = (y+1)/(x-4)

It simplifies to

x = -4/3 * (y+1) + 4

Then, reaplacing and grouping terms, etc...:

log10(I[lux]) = -4/3 * ( log10(R[kΩ])+1 ) + log10(10000)

log10(I[lux]) = log10(R[kΩ]*10)^(-4/3) + log10(10000)

log10(I[lux]) = log10 [ (R[kΩ]*10)^(-4/3) * 10000 ]

I[lux]) = (R[kΩ]*10)^(-4/3) * (10000)

I[lux] = 10000 / (R[kΩ]*10)^(4/3)

Regards

Z

 

[ArdyNT]

Ok, thank you very much.