yefj
Advanced Member level 4
Hello, a resonator which is an open circuit stripline was built as shown bellow exactly as described in the example bellow.
Smith chart and S-params and E-field are as shown bellow.
I am used to think that at resonance our S-params is supposed to very low.
Where did i go wrong?
Maybe resonance and being impedance matched is no the same thing?
Thanks.
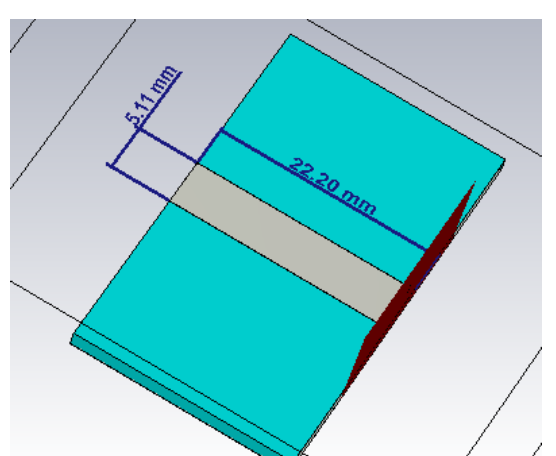
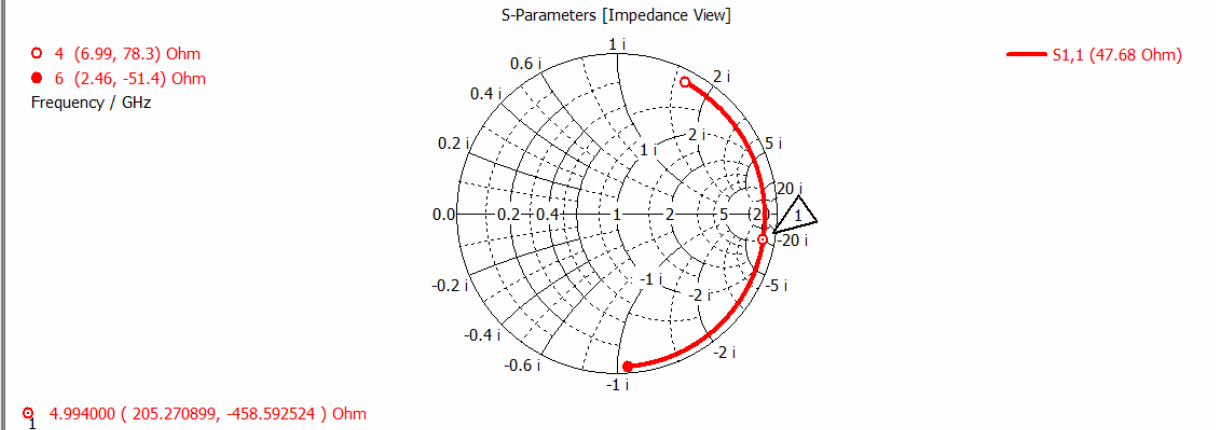

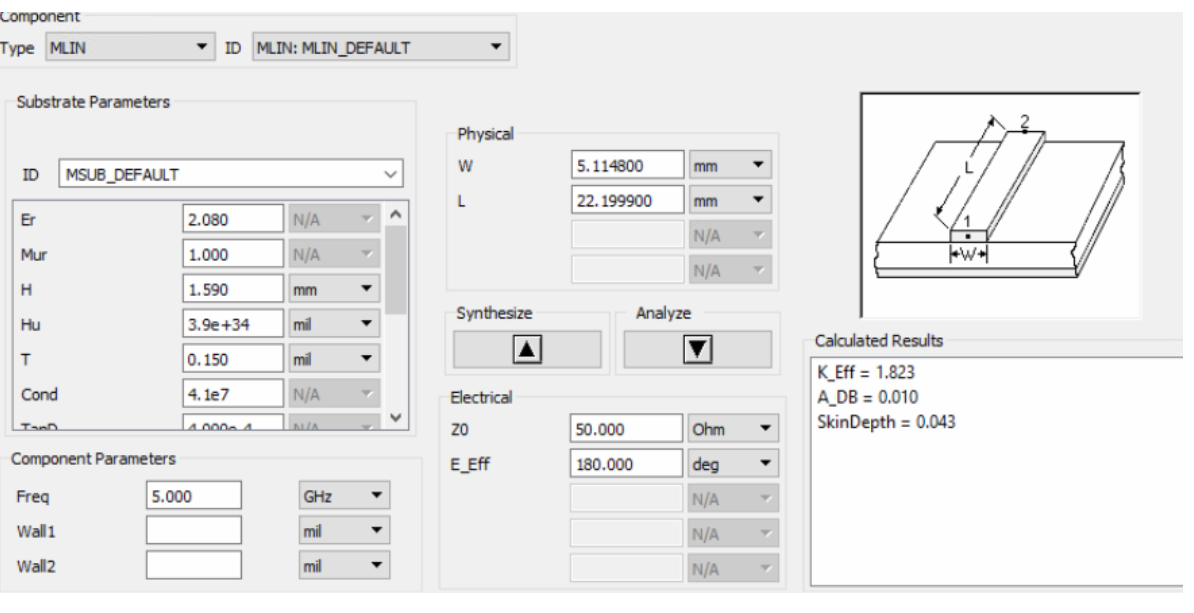
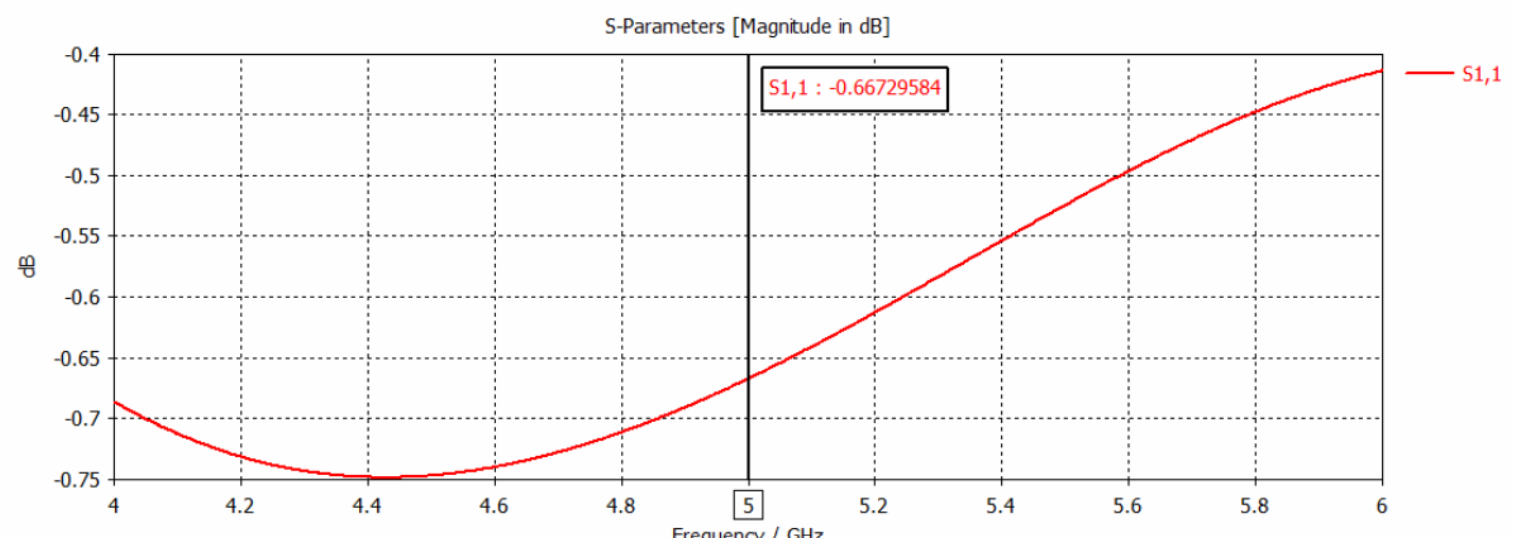

Smith chart and S-params and E-field are as shown bellow.
I am used to think that at resonance our S-params is supposed to very low.
Where did i go wrong?
Maybe resonance and being impedance matched is no the same thing?
Thanks.
