eng_ahmed_osama
Junior Member level 3

- Joined
- Feb 4, 2014
- Messages
- 29
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1
- Activity points
- 220
Hey All
I have a Question About integrator op amp
First when the Vin signal is high Vout ramp negative ( in the opposite direction)
And vice versa when Vin is low
My Question is the capacitor at the output node charge from where when the signal is high it discharge not charge , i am no explanation for that
Who the capacitor in the output node charge and discharge ???
Thanks
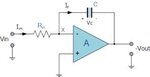
I have a Question About integrator op amp
First when the Vin signal is high Vout ramp negative ( in the opposite direction)
And vice versa when Vin is low
My Question is the capacitor at the output node charge from where when the signal is high it discharge not charge , i am no explanation for that
Who the capacitor in the output node charge and discharge ???
Thanks




