I understand, lowp-pass, high-pass, e.t.c filters but what are butterworth, bessel?

[matrixofdynamism]

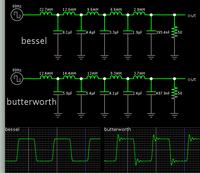
I understand the concept of low pass high pass band pass and band stop filters. However, later books talk of active filters and in that they talk of Butterworth, Chebyshev I & II, Elliptic and Bessel filters and explain the tradeoffs in pass band ripple vs stop band ripple and the roll off rate. What they never explain is how were Butterworth, Chebyshev I & II, Elliptic and Bessel filters arrived at in the first place. How were they invented? And why do books only mention these types?

 

[vGoodtimes]

These filters arise from the solution to specific optimization problems. Butterworth maximizes the "smoothness" of the frequency response. Chebychev minimizes the transition band's bandwidth for a given peak ripple in the pass/stop band. elliptic is the same, but for a peak ripple in both stop and pass bands. Bessel tries for constant "group delay", or how much frequencies within a band are delayed. In the case of Chebychev, Bessel, and Elliptic, the name comes from the functions that solve the optimization problem.

 

[Warpspeed]

Once you have determined your optimum cutoff frequency, other characteristics of the filter may be of greater or lesser importance depending on the application.

You may wish to have the sharpest possible cutoff with steepest attenuation slope, in which case a Chebychev response might be best. This works well with single sine wave frequencies.
But with complex pulse type signals, this can create ringing, and the in band response will have gain ripples. Its the most radical sharp cutoff filter.

Or you might want a much more mild and well behaved filter shape with best phase response, flatter in the pass band, and where a less steep attenuation slope will be fine for the purpose. Bessel is the least radical and best behaved type of filter.

Butterworth is a compromise between the two extremes, and is a good choice for many less demanding applications.

 

[matrixofdynamism]

Where can I find an explaination of how these filter types were invented i.e details of this "optimization problem" mentioned by you guys. The books that I have studied simply go into the subject like, this is butterworth, this is chebyshev e.t.c and this is what their response looks like, done.

No book goes into how we jump from those simple low pass high pass band pass band stop filters like the single pole filters onto these butterworth, chebyshev e.t.c types,

 

[Warpspeed]

I very much doubt you will find the information you are seeking all in one place, its a very broad topic.
Probably best to concentrate initially on either passive filters, or active filters, whichever interests you the most.

The books I have with me here, give give explanations, and some suggested values, but none go into the historical development of the subject.
I suspect the filters were named after the guys that did some original research long long ago, and then published the results.

None of the "how to" filter design text books I have read, seem to cover the historical aspect, only the practical application of the knowledge.

 

[LvW]

No book goes into how we jump from those simple low pass high pass band pass band stop filters like the single pole filters onto these butterworth, chebyshev e.t.c types,

No book? Of course, there a many books which in detail show how we arrive at the various approximations to come as close as possible to an ideal 2nd order lowpass function.
Some examples:
* Active network design (Claude Lindquist)
* Active and passive analog filters (Huelsman)
* Continuous-Time active Filter design (Deliyannis)
* Passive and Active Filters (W.K.Chen)
* Active RC Filter Design (Herpy)
* Modern Filter Design (Ghausi)
........
.........

- - - Updated - - -

I suspect the filters were named after the guys that did some original research long long ago, and then published the results.

Recently, I have seen a contribution from a very "smart" person writing "There was a man named Chebyshev who invited a very versatile filter long time ago".
This author did not know that P.L. Chebyshev (Tschebyscheff) was a russian mathematician who lived in the 19th century - long before the term "filter" even exists.

The problem is and was the following:
To approximate the ideal (brickwall) low pass filter function which can be realized with lumped components we need a broken rational function with posiitive coefficients only.
The magnitude of this function should be as close as possible to a horizontal line in the passband of the filter - and should cause a magnitude decrease (amplitude roll-off) beyond a certain selectable frequency (corner frequency, end of passband).
Thus, it is a mathematical problem which has several alternative solutions - each with some advantages and disadvantages. Hence, a trade-off is necessary (as always in electronics):

* Butterworth polynoms (named after his inventor) have a maximal flat amplitude in the passband but not a very "sharp" (it`s a bad expression) transition to the stop band.
* The mathematician P.L. Chebyshev has desribed some other polynoms (without knowing anything about filters) causing a ripple within a certain region starting with zero (defining our passband) - but with a
better transition to small values (defining our stop band).
* In some applications, it is primarily the phase (resp. the group delay) that matters for lowpass functions - and not the amplitude as in the above methods.
That means, we need a polynom (rational function) having a nearly constant group delay (linear phase) within the passband. Based on the mathematical background of the Butterworth function it is possible to find
a function with a maximum flat group delay. W.E. Thomson has used the well known Bessel functions (Mathematician F. Bessel lived in the 18th-19th century) for this purpose. The corresponding filters are called
Thomson-Bessel filter.
* A similar story applies to the elliptical functions used in Cauer filters (W. Cauer dies in 1945; he primarily was engaged in system theory and passive lumped RLC filters)

 

[schmitt trigger]

And all these great mathematicians wouldn't have been able to solve all those polynomials without the work on complex numbers by 18-century mathematician Leonhard Euler.

 

[matrixofdynamism]

I had expected these problems to be of mathematical nature in origin. So what they are trying to do is find a filter function closest to the brickwall?
How would you define a filter function? Is it a transfer function in S domain or is it a time domain function? If it is an S domain function, what does a generic filter function look like? Is it possible to have only poles and no zeros? The more poles we have at the same location the steeper role off will be and the higher the filter order will be. But this will result in filters with a huge number of components and I think this is what has been solved through these inginious methods employed as Butterworth, Chebyshev, Elliptic and Bessel. Which of those books should I study which will tell me why we get ripples when we want to have more steep roll-off?

I am aware that Elliptic and Bessel functions exist in mathematics but have not had to study them or their application. I think that the Bessel functions are related to differential equations in some way. In anycase it is not clear how the Bessel and Elliptic is related to the filters with the same name.

 

[FvM]

I believe you compiled the questionary to guide your literature rather than expecting comprehensive replies in this thread?

Some simple points can be answered though.

The discussed filter types (Bessel, buttwerworth etc.) are defined in frequency domain, obviously the typology of lowpass, highpass, bandpass also refers to it. Nevertheless you sometimes want to specify a filter in time domain, e.g. a filter converting a staircase signal to a smooth waveform with no overshoot, a typical problem when designing an arbitray function generator.

Most lowpass filters (except for Chebyshev II and elliptic) have only poles. The number of poles is the filter order. Highpass and bandpass filters need at least zeros at the origin.

It's the position of poles in complex plane that make the filter characteristic, not the poles being "at the same location".

 

[Warpspeed]

I had expected these problems to be of mathematical nature in origin. So what they are trying to do is find a filter function closest to the brickwall?.

Not always.

A brick wall filter will have a very sudden phase discontinuity in the time domain, which can produce intolerable problems with complex waveforms. It might be ideal for a narrow bandwidth radio frequency application.

A much better solution for some applications such as wide band video or serial digital data, may be a much more gradual frequency roll off, with a much better behaved phase response.

 

[matrixofdynamism]

OK, I realize that answer to my question is not going to be simple to write here. If you direct me to a specific book I will read it. Anyway, for now I will try to see what I can get in hand regarding what LvW has pointed out earlier.

 

[BradtheRad]

Comparison of bessel and butterworth filters, in their response to square waves. (Circuit found in menu of Falstad's animated simulator.)



Notice they have slightly different L & C values.

Butterworth shows a ringing effect, not normally desirable.

Bessel is made with a greater spread of L & C values. This minimizes the ringing.

It will take some digging to find out whether this was effect was found by experimentation, or predicted by Mr. Bessel's mathematics.

 

[LvW]

Comparison of bessel and butterworth filters, in their response to square waves. (Circuit found in menu of Falstad's animated simulator.)

Notice they have slightly different L & C values.
Butterworth shows a ringing effect, not normally desirable.
.

Yes - the step response of both types is a good visualization of the group delay influence: Nearly constant group delay (linear phase) for the Thomson-Bessel lowpass.
(Not shown: The lowpass damping properties in the frequency domain are not as good as for the Butterworth type).