i6power
Newbie level 3
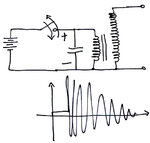
I spent 2 hours googling, but could not find any useful information on calculating the peak voltage of parallel LC tank transient response.
See the attached circuit diagram. When you open the switch, the current in L wants to keep going, and charges the capacitor, and then capacitor discharges which charges L inductor then they oscillate back and forth, each time reducing magnitude because of parasitic resistance disippating energy. What I want to know is what is the peak voltage of the first "swing"? given the values of L, C, initial voltage and parasitic resistance.
Please do not reply about resonance of LC tank circuit which is discussed in every text book, or LC series configuration.