how to calculate max flux density

[electronic4india]

hello friends ,
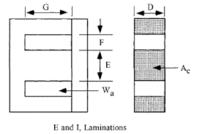
i trying to calculate push - pull smps in excellent IT software. but software need the max flux density . how to calculate max flux density or what is flux density ?
size of the core - 42*21*15 .

 

[andre_luis]

it depends on the type of material with what was manufactured the core, as well the dissipation that will be tolerated in your design, but typically it is used the value of 0,3T for calculation.

 

[treez]

0.3T is usually quoted as the saturation flux density for many ferrites. But if you do push-pull, then your flux changes polarity, and you have a large delta B. So you must make sure that your ferrite allows your flux to change by that much at the switching frequency.
There should be a databook somewhere for the ferrite which will tell you the delta B. or rather, it will enable you to work out how much the ferrite would heat up with a certain delta B/frequency.

The graphs, are, I would confess, not at all easy to analyse.

 

[andre_luis]

0.3T is usually quoted as the saturation flux density for many ferrites

In fact, and another rule of thumb is 0,1T, that is much less dissiptive for higher switching frequencies.

 

[schmitt trigger]

To answer your question correctly, you really need to know the manufacturer and the manufacturer's type for the core.

There are many ferrite materials, each optimized for a particular parameter. One of them is, of course, Bsat.

If you don't have that information, then you can be very conservative and use 0.1< Bsat <0.3 Tesla.
If you are switching at frequencies lower than 100 Khz, use 0.3 Tesla.

 

[brushhead]

Different materials have different flux densities they like to run at at varying frequencies. Personally speaking I tend not to run stuff past 200mT but that's just me. For different materials you will have different watts/kg at different frequencies and flux densities. You then need to multiply that against the volume of the core you are actually using. Then the specific heat capacity of the core should give you your heating effects. Clearly you need empirically verify your design in tests.

 

[mtwieg]

There are numerous approaches to determining Bmax and ΔB (Bmax is the peak B, ΔB is peak to peak). If you have a single ended converter like a forward converter, Bmax=ΔB is usually limited by Bsat, but in a push pull converter like a half or full bridge, the optimal 2*ΔB=Bmax is usually much lower than Bsat. In such a case, ΔB is often optimized for minimum power dissipation in the transformer, with losses coming from the core and the windings. So to calculate the optimum ΔB, you must be able to estimate those two losses.

The core losses are relatively easy, since that data is always given with the core material properties. But copper losses are much less straightforward, since there are numerous ways to wind a transformer. This is where most engineers will have to rely on nomographs provided by manufacturers, or dubious math from reference books. For example, Keith Billings provides some very useful nomographs for choosing ΔB, like in **broken link removed**. I believe this nomograph is based on the assumption that you are fully utilizing your core window with an optimal winding configuration. In his reference books he gives more nomographs on sizing conductors and number of layers and such.

Note that for a ~100W at 40KHz, you get a ΔB of under 250mT, so your Bmax will be around 125mT, much less than Bsat.

 

[treez]

Note that for a ~100W at 40KHz, you get a ΔB of under 250mT, so your Bmax will be around 125mT, much less than Bsat.

Thanks, this sounds like the spec for the Epcos TDK PM62/49 core in N87 material.

Ferrite databook of Epcos
https://en.tdk.eu/blob/519704/download/2/ferrites-and-accessories-data-book-130501.pdf

it also sounds like being from page 49 of the above databook? .....ive just noticed that says its for "ring cores", and I wonder if that still makes it applicable for say PM62/49 and other core shapes.

I appreciate that we can all only work to the data given to us, and in the case of core loss data, its always a little ambiguous, what we are served up with by the manufacturers. And of course , industries have utterly no desire for the manufacturers to make the data better presented as their competitors would then grab it.

its worth noting that page 49 of the above databook also conforms to 100degC, and ferrites can operate above 150degC, so page 49 is a little conservative...and Delta B could stretch up to further than the 125mT peak of the databook.

The article by Billings in #7 is very good, but Billings does not say what "core area product" is. I think its core cross section area multiplied by the "winding area"(?), but what the "winding area" refers to I have no idea.


Ive recently been testing a 3.5kw LLC resonant converter vin = 390vdc vout = 250-400vdc, Fsw=100khz at max load and the transformer core was tiny!....about a 6cm by 5cm ETD shaped core. it was a water cooled smps though. The transformer primary had an inductor of 74uH in parallel with it, -so that they can get the circulating current up without overheating the transformer..the 74uh inductor though was just about 3.5cm by 2.5cm by 2cm.
I just cant believe that there delta B in that tiny core was less than 400mT.

 

[mtwieg]

Thanks, this sounds like the spec for the Epcos TDK PM62/49 core in N87 material.

Ferrite databook of Epcos
https://en.tdk.eu/blob/519704/download/2/ferrites-and-accessories-data-book-130501.pdf

it also sounds like being from page 49 of the above databook?

I don't think performance factor implies the optimal Bmax for minimum loss, since it doesn't seem to take copper losses into account at all. Also I can't tell whether their Bmax refers to peak or peak to peak B.

.....ive just noticed that says its for "ring cores", and I wonder if that still makes it applicable for say PM62/49 and other core shapes.

Should be valid, since PF is just a material property.

The article by Billings in #7 is very good, but Billings does not say what "core area product" is. I think its core cross section area multiplied by the "winding area"(?), but what the "winding area" refers to I have no idea.

As the article states, "it may be obtained by multiplying the center core pole area by the available winding window area in centimeters." So winding area is just the max crossectional area all your windings may occupy.

 

[treez]

As the article states, "it may be obtained by multiplying the center core pole area by the available winding window area in centimeters." So winding area is just the max crossectional area all your windings may occupy.

so this is the cross sectional area of the centre spindle of the bobbin? Otherwise each layer of windings would not occupy the same area, as the top ayers ccupy bigger area overall, because they are sitting on the bottom layers.?

- - - Updated - - -

Also I can't tell whether their Bmax refers to peak or peak to peak B.

if yourself also are saying this , then I am going to write to them to ask for clarification.

 

[mtwieg]

so this is the cross sectional area of the centre spindle of the bobbin? Otherwise each layer of windings would not occupy the same area, as the top ayers ccupy bigger area overall, because they are sitting on the bottom layers.?

That's a different cross section. Take an example from an EI core:



So window area Wa=F*G, core area Ac=D*E, so area product Ap=F*G*D*E.

if yourself also are saying this , then I am going to write to them to ask for clarification.

If you get an answer, please let us know.