Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.

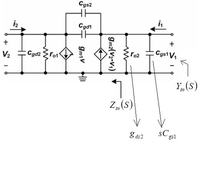

(2) is (1) written with matrices, just hard to make matrices with text, plus multiple spaces are stripped from your formatting so the result is hard to understand.Hi dgnani
I try to do your calculation at #8 answer, but I cant understand how you write (2) from (1) :sad:

oh sorry I wrote wrongI mean Y(S)
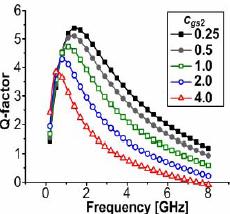
ok then with this 2 assumption I can drive your final Y(S) equation, now Is this Y(S) valid for all range of frequency or it is valid just for low frequency?