shomikc
Member level 4
Can anybody please give me the algorithm or procedure to find the Fourier series or transform of a quasiperiodic signal. Thankyou.
I need this for homework that I would like to give my students. I am not able to proceed as the signal is not a regular signal like a triangular or square where the function of the signal is defined.
This is what the signal looks like.
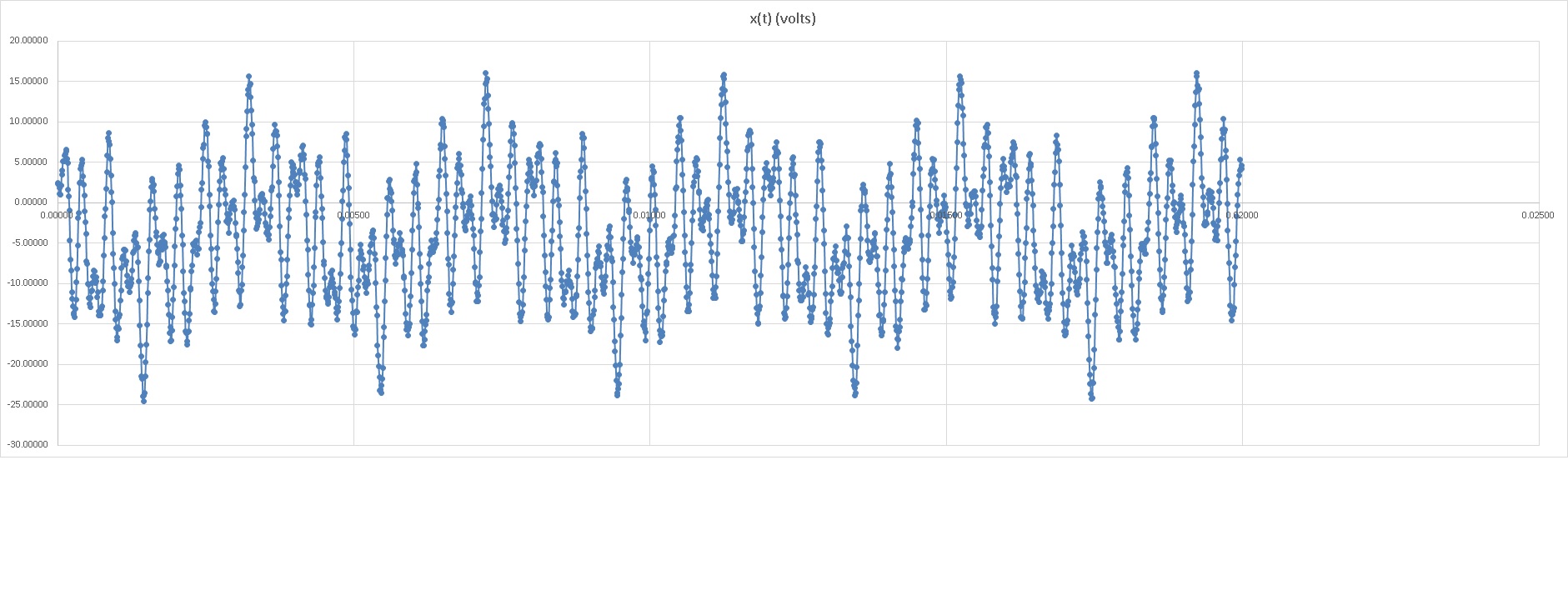
There are 5 periods of 400 points each, a total of 2000 points, and I need to find the coefficients upto 20th harmonic. I also have to identify the dc component and the 4 largest frequency components. Please help.
The complete question is given here.

I need this for homework that I would like to give my students. I am not able to proceed as the signal is not a regular signal like a triangular or square where the function of the signal is defined.
This is what the signal looks like.
There are 5 periods of 400 points each, a total of 2000 points, and I need to find the coefficients upto 20th harmonic. I also have to identify the dc component and the 4 largest frequency components. Please help.
The complete question is given here.

