JupiW
Newbie level 1

- Joined
- Aug 25, 2009
- Messages
- 1
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,281
- Activity points
- 1,291
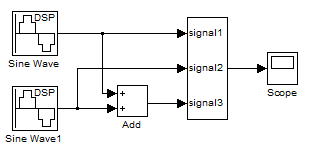
x(t) = Sin(2t) + Sin(3t)
Thnx
Thnx
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.





If the example were sin(2t)+sin(0.5t), then you would have a period of 4pi (seconds). likewise sin(2t) + sin(6t) would be periodic with pi (seconds). sin(6t) + sin(10t) would have a period of pi (seconds) as well. Using these examples, it should be easy to find the answer to what appears to be a homework question.
For sin(w*t), w would be an angular frequency (rad/second), not a period.


The period of the sum of periodic signal is given by the least common multiple (lcm) among the periods of each signal.
In your example: x(t) = Sin(2t) + Sin(3t)
sin (and cos) function complete a period every 2Π rad, then (supposing to start from 0 rad):
2•t1=2Π --> t1=Π
3•t2=2Π --> t2=2•Π/3
to find lcm you have to ignore the denominator if it is an integer and take the factor having maximum exponent at the two numerators. In this case we have the factors Π (numerator of t1), 2 and Π (numerator of t2) so I'll take Π only once and 2.
lcm=2•Π ==> the period of x(t) will be 2•Π
As another example, let's consider x(t) = sin(1.3t)+sin(3t)
1.3•t1=2Π --> t1=2Π/1.3 --> I have to transform the denominator into integer --> t1=20Π/13
3•t2=2Π --> t2=2Π/3
The lcm (an then the period) will be now 20Π
factors were 2²,5,Π and 2,Π so I'll take 2²,5,Π