Negneg
Newbie level 6
Hi,
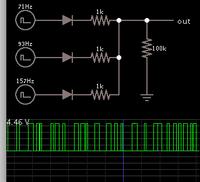
I'm trying to generate 100 different source LFSR signals (just to have random 0/1 inputs) to give to a NAND gate as input in HSpice. Is there any way to generate such wave in a loop or something? For example a way to change the taps numbers ( [5, 2] to different numbers in vin1 and/or add more taps like [10, 5, 3, 2] in vin2 in the examples below) in a loop to get 100 different waves. I tried using sweep and monte, however I'm not sure if they are actually helpful!
Thanks!
I'm trying to generate 100 different source LFSR signals (just to have random 0/1 inputs) to give to a NAND gate as input in HSpice. Is there any way to generate such wave in a loop or something? For example a way to change the taps numbers ( [5, 2] to different numbers in vin1 and/or add more taps like [10, 5, 3, 2] in vin2 in the examples below) in a loop to get 100 different waves. I tried using sweep and monte, however I'm not sure if they are actually helpful!
Code:
.tran .1ps 10ns
Vin1 in1 0 LFSR (0 0.9 0 10p 10p 10e+9meg 1 [5, 2])
Vin2 in2 0 LFSR (0 0.9 0 10p 10p 10e+9meg 1 [10, 5, 3, 2])
Last edited by a moderator: