gonsays
Newbie level 5
Hello guys,
I'm having a problem understanding the values of the solution for the following question amd circuit:

The solution is:
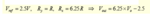
What are the equations used in order to get those values?
What would be the best strategy to analyze the circuit?
Thank you very much in advance! Any info is appreciated
I'm having a problem understanding the values of the solution for the following question amd circuit:

The solution is:
What are the equations used in order to get those values?
What would be the best strategy to analyze the circuit?
Thank you very much in advance! Any info is appreciated
