yefj
Advanced Member level 4
Hello,i need to drive 5 such mosfets as shown in the simulation below.
Each mosfet draws 15A when the pulse opens the mosfet.
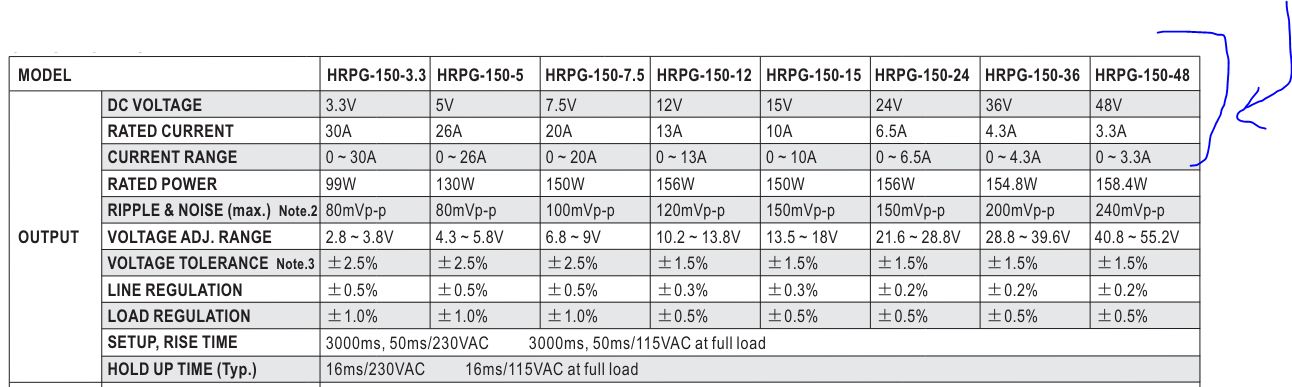
My power supply is gives the 48V but only 3.3A,If I understand correctly I need to put very high decoupling capacitors at the voltage source footprint so I will have in that short period of time the 5*15=75A I need.
Is there a theory which could explain me the logic of this trick?
What kind of capacitors do you recommend me to use?
Thanks.
https://www.meanwell-web.com/content/files/pdfs/productPdfs/MW/HRPG-150/HRPG-150-spec.pdf
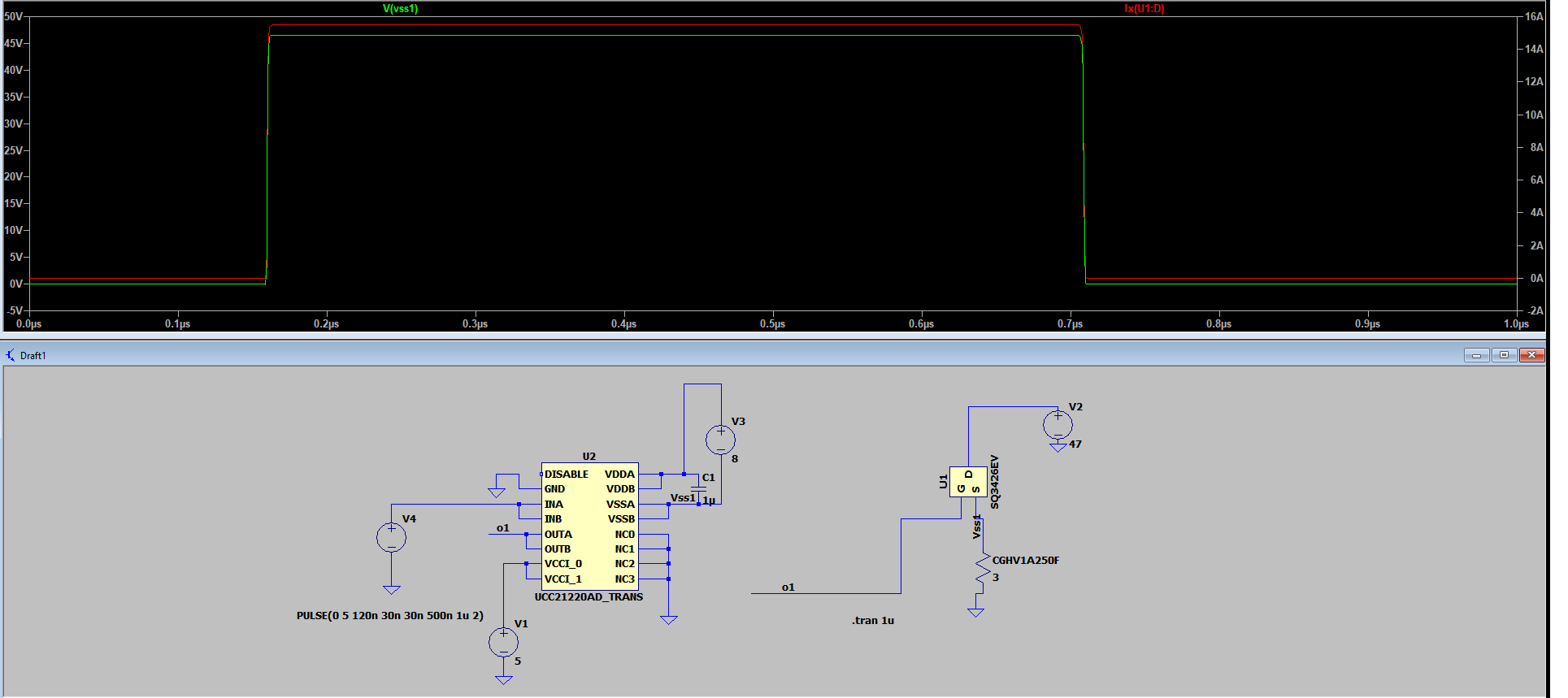
Each mosfet draws 15A when the pulse opens the mosfet.
My power supply is gives the 48V but only 3.3A,If I understand correctly I need to put very high decoupling capacitors at the voltage source footprint so I will have in that short period of time the 5*15=75A I need.
Is there a theory which could explain me the logic of this trick?
What kind of capacitors do you recommend me to use?
Thanks.
https://www.meanwell-web.com/content/files/pdfs/productPdfs/MW/HRPG-150/HRPG-150-spec.pdf