bandwidth of the unity gain buffer

[Junus2012]

Dear friends

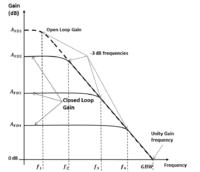
Kindly, why the bandwidth of the unity gain op-amp buffer is defined at the unity gain frequency, while the bandwidth at any different gain is at -3db.

if I apply this principle on the buffer op-amp, then the bandwidth is 0 dB-3 dB = - 3 dB not at 0 dB as from GBW

thank you

 

[rakshitdatta]

It is always -3 dB bandwidth that is specified whether it is unity gain or gain greater than one. However, it so happens in a unity gain buffer(non inverting configuration) that the unity gain frequency of the opamp transfer function(open loop transfer function) will be same as the -3 dB bandwidth of the unity gain buffer(close loop transfer function).

 

[Junus2012]

Could you please show me in any graph th -3 dB frequency of the buffer connected op-amp please

It is always -3 dB bandwidth that is specified whether it is unity gain or gain greater than one. However, it so happens in a unity gain buffer(non inverting configuration) that the unity gain frequency of the opamp transfer function(open loop transfer function) will be same as the -3 dB bandwidth of the unity gain buffer(close loop transfer function).

 

[LvW]

Could you please show me in any graph th -3 dB frequency of the buffer connected op-amp please

Junus - it is very simple:

For any first-order circuit the 3dB point is at a frequency where both imaginary and real part of the denominator are equal. This applies also to the simple RC lowpass.
The denominator of the gain for buffer is D(s)=1/Ao + beta.
With beta=1 (100% feedback) and 1/Ao=j at the transit frequency wt the magnitude of the denominator is SQRT(2)=1.414.
This gives an overall gain drop of -3dB.
(Remember: Open-loop gain approximation Ao=wt/jw )

 

[Junus2012]

Thanks LvW,

but the gain of the buffer connected start from 0 dB, so I am unable to imagine how the concept of -3 dB is applied here, please see this image

Junus - it is very simple:

For any first-order circuit the 3dB point is at a frequency where both imaginary and real part of the denominator are equal. This applies also to the simple RC lowpass.
The denominator of the gain for buffer is D(s)=1/Ao + beta.
With beta=1 (100% feedback) and 1/Ao=j at the transit frequency wt the magnitude of the denominator is SQRT(2)=1.414.
This gives an overall gain drop of -3dB.
(Remember: Open-loop gain approximation Ao=wt/jw )

 

[erikl]

... the gain of the buffer connected start from 0 dB, so I am unable to imagine how the concept of -3 dB is applied here

Junus,

as you can see from your diagram, the -3dB frequencies are different from their GBW frequencies (gain = 0dB). So for a buffer (gain = 0dB) you can't really speak of a GBW (you could perhaps "define" it somewhat arbitrarily for its gain crossing, e.g., the -0.1dB line, or the -3dB line). This latter -3dB frequency, however, is clearly defined for a buffer, too. So usually for a buffer its -3dB frequency is also called its GBW - they are identical.

 

[Junus2012]

Dear erikl and LvW

I apologize first from you both because I usually make you busy with my stupid questions that I must known from the elementary class. any way, returning back to my question

Here I plot the -3 dB frequency of the buffer connection, if it is right, then the GBW as seen from the image is different from the -3 dB frequency connection, as a result, the bandwidth of the buffer conection is beyond the GBW not exactly the GBW

Junus,

as you can see from your diagram, the -3dB frequencies are different from their GBW frequencies (gain = 0dB). So for a buffer (gain = 0dB) you can't really speak of a GBW (you could perhaps "define" it somewhat arbitrarily for its gain crossing, e.g., the -0.1dB line, or the -3dB line). This latter -3dB frequency, however, is clearly defined for a buffer, too. So usually for a buffer its -3dB frequency is also called its GBW - they are identical.

 

[rakshitdatta]

Junus,

Let us assume that the open loop transfer function(i.e., the opamp input-output transfer function) is A(jw). In the figure, the dotted line shows this transfer function. Now, let us assume that we connect this opamp in a unity gain buffer configuration(non inverting). Now, the buffer is a feedback circuit. The closed loop transfer function(the "buffer" input-output transfer function), by principle of the negative feedback, is given as A(jw)/(1+A(jw)). Let us evaluate this transfer function at w=GBW(as shown in the figure). At w=GBW, the magnitude of A(jw) = 1. Therefore, the closed loop transfer function will have a magnitude of 1/sqrt(2). In dB scale, 1/sqrt(2) corresponds to -3 dB. Hence, the - 3dB bandwidth of the closed loop transfer function will be the same as GBW of the open loop transfer function