back EMF cancelation

[Salvador12]

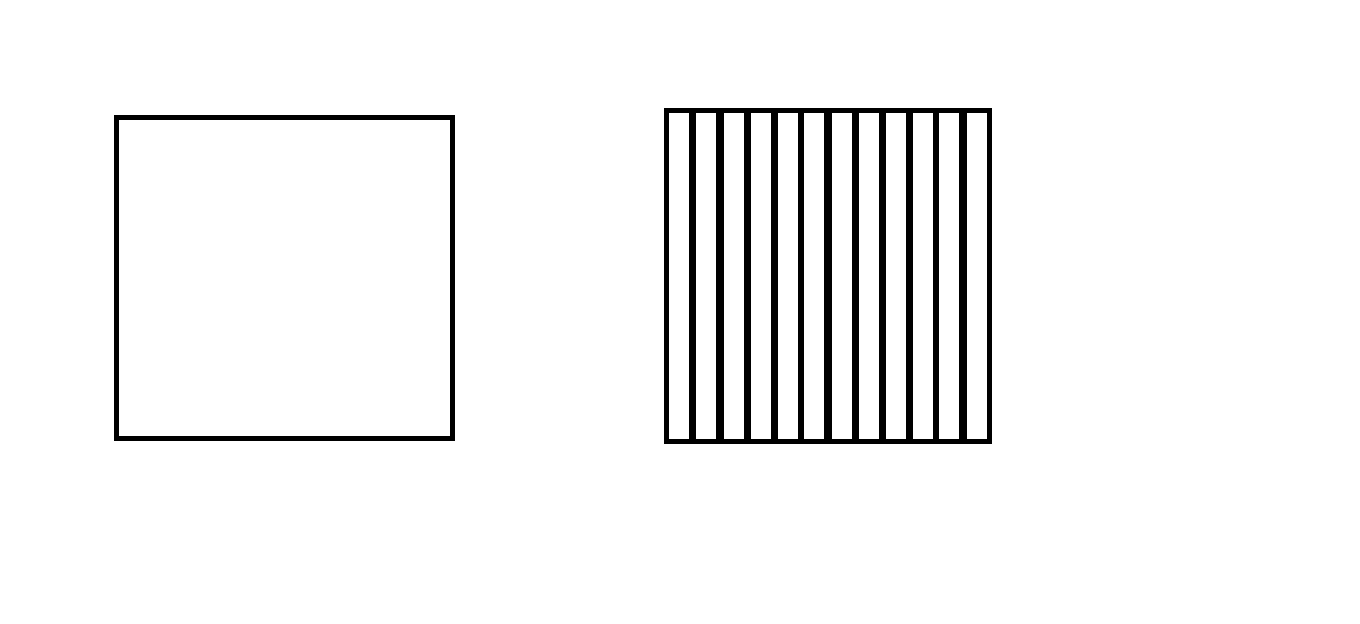
I want to know one thing. If we have a simple loop like the rectangular loop shown on the left side in the attached picture, if there is a magnetic field that changes through it it induces a current in the loop. What if we apply the same field to the loop on the right side that consists of multiple parallel loops that all share one of their conductors?

Theoretically induction in each of the parallel loops should be zero because the shared conductors means that current within one loop would want to travel say upwards through the shared conductor while current in the adjacent loop would flow downwards and vice versa which should lead to total cancellation if each loop is identical.

What happens with the total loop that is enclosed by the outermost conductors of each smaller loop within the rectangle?
Because if you take out the smaller loops there is still the large single loop like on the left side. But I would think that with the paralleled smaller loops inside the larger loop should also get no induced EMF?

 

[FvM]

Side remark, IMHO the term back-EMF is inappropriate for induced current in a closed conductor.

To analyze current distribution in the multi-conductor configuration, field geometry must be known. In case of a homogen field perpendicular to the loop area, current in the center trace is probably canceled, all other traces carry some current. Depending on trace resistance, there will be also a partial field displacement out of the loop area.

All-in-all I'd opt for FEM analysis rather than conclusions.