daifancer
Newbie
The pole-zero properties of common-source amplifiers are introduced in Chapter 6.2 of Razavi's <<Design of Analog CMOS Integrated Circuit >>. The book explains why zero points occur:
"
CGD provides a feedforward path that conducts the input signal to the output at very high frequencies,resulting in a slope in the frequency response that is less negative than -40dB/dec......
"
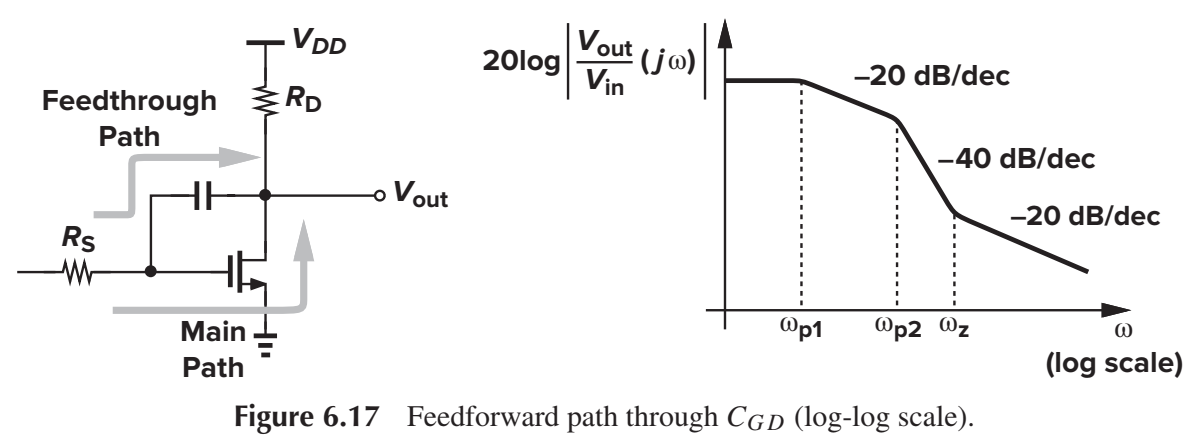
From this point of view to understand the generation of zeros is relatively easy.
The problem is, then, that the book introduces a new way of calculating zero points:
"
The zero, sz, can also be computed by noting that the transfer function Vout(s)/Vin(s) must drop to zero for s = sz. For a finite Vin, this means that Vout(sz) = 0, and hence the output can be shorted to ground at this (possibly complex) frequency with no current flowing through RD or the short (Fig. 6.18).Therefore, the currents through CGD and M1 are equal and opposite:
V1*CGD*sz = gm*V1
"
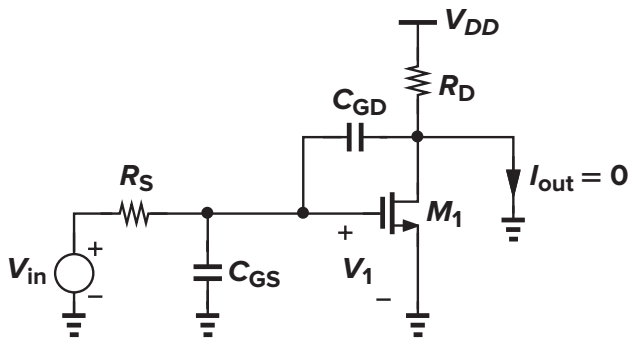
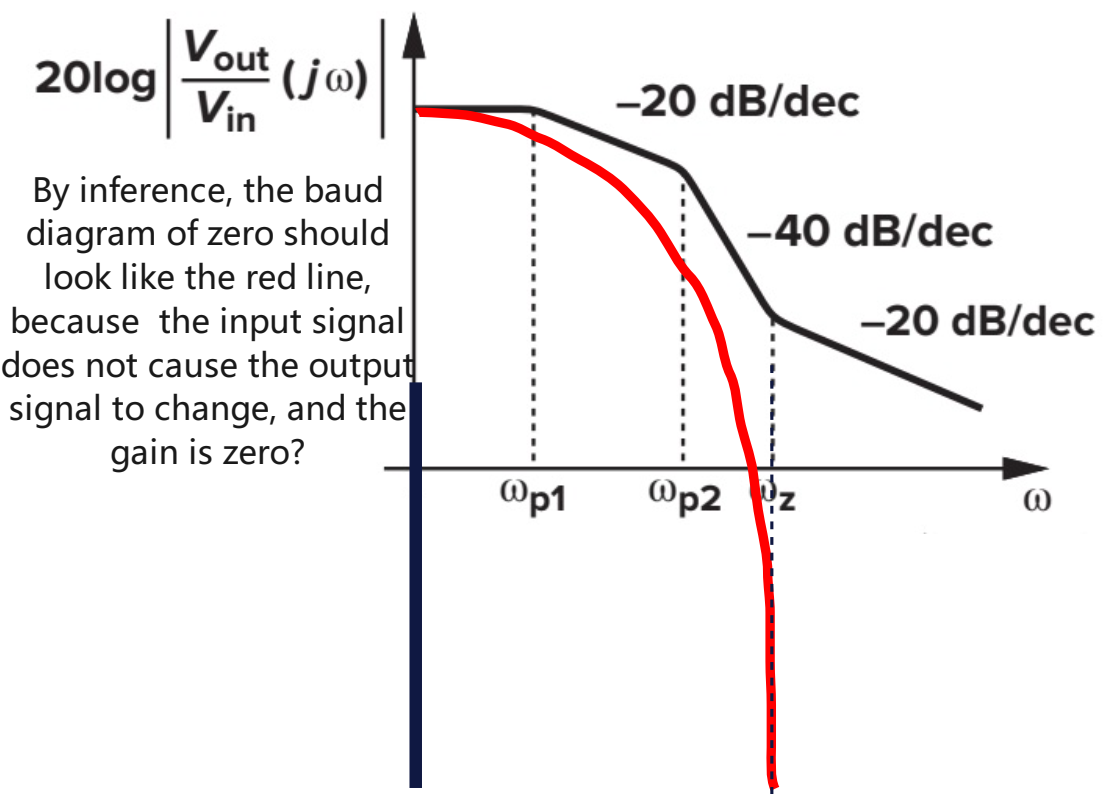
From the above , does it mean that when the input frequency is zero frequency gm/CGD , and the voltage change at the output is zero? Lead to the the transfer function H (s) at this freq is zero? Thus you get a amplitude-response of minus infinity on the Bode-Plots?
Clearly this conclusion is not true, but what is wrong with the inference process above? Or is there something missing?
"
CGD provides a feedforward path that conducts the input signal to the output at very high frequencies,resulting in a slope in the frequency response that is less negative than -40dB/dec......
"
From this point of view to understand the generation of zeros is relatively easy.
The problem is, then, that the book introduces a new way of calculating zero points:
"
The zero, sz, can also be computed by noting that the transfer function Vout(s)/Vin(s) must drop to zero for s = sz. For a finite Vin, this means that Vout(sz) = 0, and hence the output can be shorted to ground at this (possibly complex) frequency with no current flowing through RD or the short (Fig. 6.18).Therefore, the currents through CGD and M1 are equal and opposite:
V1*CGD*sz = gm*V1
"
From the above , does it mean that when the input frequency is zero frequency gm/CGD , and the voltage change at the output is zero? Lead to the the transfer function H (s) at this freq is zero? Thus you get a amplitude-response of minus infinity on the Bode-Plots?
Clearly this conclusion is not true, but what is wrong with the inference process above? Or is there something missing?