466576266
Member level 1
- Joined
- Mar 22, 2010
- Messages
- 36
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,286
- Location
- ShangHai,China
- Activity points
- 1,541
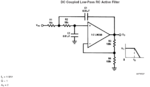
hey, recently i am designing an active filter circuit. but i meet with a problem. as u can see the pic, the fliter chip is from the national semiconductor. well, the focus is the calculation.
i know how to calculate two fo them: Fo=1/2*3.14*R1*C1
Av=1+R3/R4
But how to calculate the Q, and what is real meaning ? anybody can solve this problem, and some materials related with the Q is ok.
thanks in advance.
i know how to calculate two fo them: Fo=1/2*3.14*R1*C1
Av=1+R3/R4
But how to calculate the Q, and what is real meaning ? anybody can solve this problem, and some materials related with the Q is ok.
thanks in advance.