julian403
Full Member level 5

For a transistor likes:
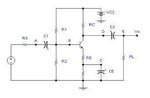
the DC load lines is:
\[Ic(sat) = \frac{Vcc}{Rc+Re}\]
and
\[Vce(sat) = Vcc\]
and the current is
\[Ic = - \frac {Vce}{Re+Rc} \]
And de AC load line:
\[ic(sat) =\frac{Vcc}{Rc+Re} + \frac{vce}{Rc//Rl}\]
So, that the same as
\[\frac{Vce}{x} =\frac{Vcc}{Rc+Re} + \frac{vce}{Rc//Rl}\]
What would x ?

the DC load lines is:
\[Ic(sat) = \frac{Vcc}{Rc+Re}\]
and
\[Vce(sat) = Vcc\]
and the current is
\[Ic = - \frac {Vce}{Re+Rc} \]
And de AC load line:
\[ic(sat) =\frac{Vcc}{Rc+Re} + \frac{vce}{Rc//Rl}\]
So, that the same as
\[\frac{Vce}{x} =\frac{Vcc}{Rc+Re} + \frac{vce}{Rc//Rl}\]
What would x ?

