Kodomer
Newbie level 3

Hello,
I am building a 2.4 GHz Yagi-Uda directional antenna for Wifi. I use a RG-58/U coaxial cable with 50 Ohm. I use the Yagi calculator of VK5DJ as a guide: https://www.vk5dj.com/yagi.html
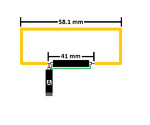
The folded dipole has an impedance of 288 Ohm. The transmission line has an impedance of 50 Ohm. The impedances do not match, so impedance matching is needed to avoid power loss due to reflection.
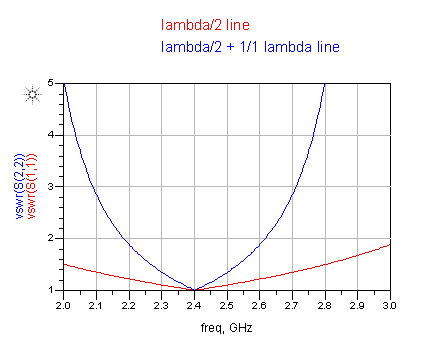
For 2442 MHz the Yagi calculator of VK5DJ recommends a 4.1 cm long RG-58C coaxial cable as a Balun.
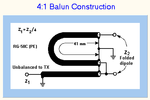
Unfortunately the minimum bending radius of RG-58/U coaxial cable is 25.4 mm. Bending a 4.1 cm long RG-58/U for 180 degrees violates the minimum bending radius and probably changes the properties of the cable. Now I understand why it is a calculator for VHF/UHF. Now I am stuck.
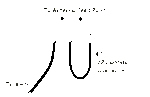
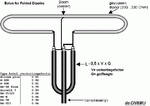
I have an idea how to avoid bending the 4.1 cm coax cable for 180 degree. But this requires that the core of cable A is at least 4.1 cm shorter than the shield of this cable. But does this changes the properties of the coax cable?
Or should I use conductors and capacitors instead of a coaxial cable for impedance matching?
I am stuck. This is the first antenna I am building and don't know how to continue.
I am building a 2.4 GHz Yagi-Uda directional antenna for Wifi. I use a RG-58/U coaxial cable with 50 Ohm. I use the Yagi calculator of VK5DJ as a guide: https://www.vk5dj.com/yagi.html
The folded dipole has an impedance of 288 Ohm. The transmission line has an impedance of 50 Ohm. The impedances do not match, so impedance matching is needed to avoid power loss due to reflection.
For 2442 MHz the Yagi calculator of VK5DJ recommends a 4.1 cm long RG-58C coaxial cable as a Balun.

Unfortunately the minimum bending radius of RG-58/U coaxial cable is 25.4 mm. Bending a 4.1 cm long RG-58/U for 180 degrees violates the minimum bending radius and probably changes the properties of the cable. Now I understand why it is a calculator for VHF/UHF. Now I am stuck.
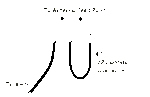

I have an idea how to avoid bending the 4.1 cm coax cable for 180 degree. But this requires that the core of cable A is at least 4.1 cm shorter than the shield of this cable. But does this changes the properties of the coax cable?

Or should I use conductors and capacitors instead of a coaxial cable for impedance matching?
I am stuck. This is the first antenna I am building and don't know how to continue.