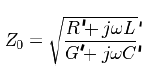DeboraHarry
Full Member level 5

I have a transmission line, which is like coax cable, but has a deliberately poor shield, so it will radiate. I'm trying to analyse this in HFSS. What's the best way to find the impedance of the coax? Since the cable is not lossless, the impedance will be complex, and of course vary with frequency.
Deborah
Deborah