lawfulgm
Junior Member level 2

Hi all,
in high-speed serial link design, we usually see more # of post-cursor ISI than pre-cursor ISI.
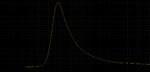
The attachment is output pulse response of s-parameter channel I have. input is an ideal pulse with bit rate of 25 Gbps.
As shown in the attachment, we see that slope of rising edge is clearly faster than the slope of falling edge.
Does anyone know why this happens from physics perspective?
Thanks,
in high-speed serial link design, we usually see more # of post-cursor ISI than pre-cursor ISI.
The attachment is output pulse response of s-parameter channel I have. input is an ideal pulse with bit rate of 25 Gbps.
As shown in the attachment, we see that slope of rising edge is clearly faster than the slope of falling edge.
Does anyone know why this happens from physics perspective?
Thanks,