why transmission line can not receive EM wave?

[xuexucheng]

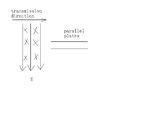
In free space, the TEM wave can transmit.

In a pair of parallel plates (transimision line), the mode is also TEM.

Why can not we use the parallel plates to receive the wave?
Why?

you may say the impedance is not match. but how can they be matched?

I find there is no any context about this in textbook.

Thank you very much.

 

[PlanarMetamaterials]

Look up information on antennas.

They are nothing more than devices which match transmission lines to free space.

I suggest Antenna Theory by Balanis

 

[thylacine1975]

Seconding PlanarMetamaterials, the antenna provides a transition from the mode of propagation within the waveguide to that in free space.

Naturally, a freely propagating wave *outside* the transmission line cannot be 'received' by the line because of the boundary conditions (such as electrically conductive parallel plates) that serve to contain an EM mode within the transmission line in the first place also serve to exclude the affects of external fields. At the 'ends' of the transmission line (such as at the 'edges' of a set of infinite parallel plates these boundary conditions are relaxed, and at this point coupling to/fro free space may occur. Typically this process is extremely inefficient as the overlap integral between the guide/free space mode (in optics parlance) or impedance match between the guide/free space Z (from a radio perspective) is small/poor. This is where an antenna/lens helps.

Note the word 'helps' though... some coupling - albeit inefficient - *does* occur directly into the transmission line as described above. For example, wave the ports of a vector network analyser near each other and observe the coupling. Alternatively, the fact that you can see the red light spraying out of the end of your audio system's TOSLINK fibre illustrates the same effect.

 

[xuexucheng]

Your response is very helpfull.
because of the boundary conditions
----------- I do not think there is boundary condition different between free space and transmision line.
Could you explain the boundary conditions in detail?
Thank you

Seconding PlanarMetamaterials, the antenna provides a transition from the mode of propagation within the waveguide to that in free space.

Naturally, a freely propagating wave *outside* the transmission line cannot be 'received' by the line because of the boundary conditions (such as electrically conductive parallel plates) that serve to contain an EM mode within the transmission line in the first place also serve to exclude the affects of external fields. At the 'ends' of the transmission line (such as at the 'edges' of a set of infinite parallel plates these boundary conditions are relaxed, and at this point coupling to/fro free space may occur. Typically this process is extremely inefficient as the overlap integral between the guide/free space mode (in optics parlance) or impedance match between the guide/free space Z (from a radio perspective) is small/poor. This is where an antenna/lens helps.

Note the word 'helps' though... some coupling - albeit inefficient - *does* occur directly into the transmission line as described above. For example, wave the ports of a vector network analyser near each other and observe the coupling. Alternatively, the fact that you can see the red light spraying out of the end of your audio system's TOSLINK fibre illustrates the same effect.

 

[thylacine1975]

The boundary conditions are imposed by the 'boundaries' (i.e. the spatial position of the plates defining the extent) of the transmission line.
For example: visualise two parallel plates of (we'll assume perfectly conductive) metal extending to infinity in the XY plane, spaced (say 1mm) apart such that one plane was at Z = 0 [mm], and the other at Z = 1 [mm]. A TEM wave propagating between the plates is completely invisible to an observer sitting above them at (x=0, y=0, z = 5), for instance. Similarly (by reciprocity), the observer cannot influence the TEM wave travelling between the plates beneath his feet from his position either. (i.e. no transmission/reception/coupling to free space from the transmission line).

Why is this the case? Because the plates are perfectly conductive, there cannot exist any electric field component tangential (i.e. in the same plane) as the plates in the same place they are. If you tried to establish a field gradient parallel to the plate, it would be "shorted out" by the perfect conductor. (Perfect conductor = zero resistance = zero voltage differential irrespective of the induced current). Consequently, only an electric field component *normal* to the plates can exist in their proximity - which gives rise to the only propagating modes between them as the solutions to the wave equation describing the classic TE, TEM and TEM modes. A wave propagating in the free space (where we refer to it being unbounded - i.e. having infinite extent in the case of plane waves, or only loosely constrained in the case of optical Gaussian modes) outside the plates cannot pass through the plates for the same reasons. If the incident wave induces a current in the plate surface as a result of having an electric field component parallel/tangential to the plate, this current causes re-radiation (appearing as a reflection) from the incident surface. Nothing appears on the other side of the plate - it has imposed a "boundary".

I hope that makes some semblance of sense! Unfortunately, most introductions to EM propagation leap straight into a world of div, grad & curl without offering any intuitive insight into the processes going on... sure, it's all there in the vector maths, but I personally couldn't make head or tail of it until I could imagine some physical models to attach it all to - good luck

P.S. What happens if they're *not* perfectly conductive... like copper...? The analysis rapidly gets messy in conductive media and all sorts of interesting effects arise such as the electric field component can now be non-zero at the plate boundary (tiny, sure - but not zero, owing to their finite resistance). This allows an (exponentially decaying) magnitude to exist throughout the metal thickness which gives rise to coupling through the plates etc etc. Lots of fascinating applications! (Underwater comms, for example).

 

[zorro]

Think in an ideal, uniform and infinite transmission line.
It "guides" a wave in TEM mode but it does not radiate i.e., it does not transfer energy to free space in the form of electromagnetic radiation. In other words, it is bad as a transmitting antenna.
Because of reciprocity, it is a bad receiving antenna too.

Now, suppose that you cut the line. At the cut point, only a very small part of the energy of the guided wave is radiated. Almost all is reflected.
In order to have a transfer of energy to free sace (i.e. radiation) you need something that makes the interface between the TEM mode of the line and the TEM mode of free space. (Both modes are TEM but have very different configurations of E and M fields.)
That something is an antenna.

Regards

Z

 

[xuexucheng]

Thank you very much.
Your answer is very helpfull to me.
My really question may be expressed using the figure below.
The left is TEM wave in free space. and the right is parallel plates.
I think the directions of the E and H can satisfy the parallel plates. Why we can not receive TEM mode wave in the plates?

A wave propagating in the free space (where we refer to it being unbounded - i.e. having infinite extent in the case of plane waves, or only loosely constrained in the case of optical Gaussian modes) outside the plates cannot pass through the plates for the same reasons. If the incident wave induces a current in the plate surface as a result of having an electric field component parallel/tangential to the plate, this current causes re-radiation (appearing as a reflection) from the incident surface. Nothing appears on the other side of the plate - it has imposed a "boundary".

I hope that makes some semblance of sense! Unfortunately, most introductions to EM propagation leap straight into a world of div, grad & curl without offering any intuitive insight into the processes going on... sure, it's all there in the vector maths, but I personally couldn't make head or tail of it until I could imagine some physical models to attach it all to - good luck

P.S. What happens if they're *not* perfectly conductive... like copper...? The analysis rapidly gets messy in conductive media and all sorts of interesting effects arise such as the electric field component can now be non-zero at the plate boundary (tiny, sure - but not zero, owing to their finite resistance). This allows an (exponentially decaying) magnitude to exist throughout the metal thickness which gives rise to coupling through the plates etc etc. Lots of fascinating applications! (Underwater comms, for example).

 

[PlanarMetamaterials]

I think the directions of the E and H can satisfy the parallel plates. Why we can not receive TEM mode wave in the plates?

The boundary condition is an impedance mismatch. Applying the definition of impedance, you can see that in the two mediums, the E/H ratio is not the same, so you can't just expect the wave to continue through the boundary uninterrupted.

 

[StergiosP]

I think the directions of the E and H can satisfy the parallel plates. Why we can not receive TEM mode wave in the plates?
View attachment 86974

Basically, you can get a TEM mode between the plates BUT the energy coupled to this mode would be too small compared to the energy of the free space TEM mode (very poor coupling efficiency). This is because of the impedance mismatch as other people have already said.
Your confusion starts from the fact that you think that you cannot receive any signal in the parallel plate configuration when in fact this is not totally true. You just get a very small fraction of the "incoming wave" propagating along the PP waveguide.

 

[zorro]

...
My really question may be expressed using the figure below.
The left is TEM wave in free space. and the right is parallel plates.
I think the directions of the E and H can satisfy the parallel plates. Why we can not receive TEM mode wave in the plates?
**broken link removed**

Ah, I believe I see your point now.

This is my point of view:
Suppose you have a plane wave propagating from left to right, like in your picture.
If a conductive plate is placed orthogonal to the E field, like in the picture, the propagation of the wave doesn't change at all. (The plate can be finite or semi-infinite.)
Place now a second plate parallel to the first one. The wave continues without change. We have E and H fields between the plates and outside as well.
In that condition, a voltage is developed between the two plates and its available power V²/Z₀ can be delivered to a load (eventually by means of a transition). This is an antenna receiving the wave.

Interesting discussion.
Regards

Z

 

[xuexucheng]

Do you think that a voltage is developed between the two plates?
But I have never kown this type of antenna.
I estimate that the plates can not receive voltage.

Ah, I believe I see your point now.

This is my point of view:
Suppose you have a plane wave propagating from left to right, like in your picture.
If a conductive plate is placed orthogonal to the E field, like in the picture, the propagation of the wave doesn't change at all. (The plate can be finite or semi-infinite.)
Place now a second plate parallel to the first one. The wave continues without change. We have E and H fields between the plates and outside as well.
In that condition, a voltage is developed between the two plates and its available power V²/Z₀ can be delivered to a load (eventually by means of a transition). This is an antenna receiving the wave.

Interesting discussion.
Regards

Z

- - - Updated - - -

the E/H ratio is same in free space and parallel plates if the matter between the plates is air.

The boundary condition is an impedance mismatch. Applying the definition of impedance, you can see that in the two mediums, the E/H ratio is not the same, so you can't just expect the wave to continue through the boundary uninterrupted.

- - - Updated - - -

impedance mismatch
-- I do not understand. first we must know the defination of impedance.
in free space is E/H, But in tansmission line is V/I. But in free space and in transmission line(air between the plates) the E/H is SAME.

Basically, you can get a TEM mode between the plates BUT the energy coupled to this mode would be too small compared to the energy of the free space TEM mode (very poor coupling efficiency). This is because of the impedance mismatch as other people have already said.
Your confusion starts from the fact that you think that you cannot receive any signal in the parallel plate configuration when in fact this is not totally true. You just get a very small fraction of the "incoming wave" propagating along the PP waveguide.

 

[zorro]

Do you think that a voltage is developed between the two plates?

Yes, considering only the plates. (I mean, without considering the load and the transition referred in the next paragraph.)

But I have never kown this type of antenna.

Well. I mentioned a transition needed for the energy transfer between the pair of plates to the load.
A suitable standard method to connect a load is, for example, by means of a rectangular waveguide in TE10 mode. We need then a transition between the couple of plates to the waveguide, in such a way that the TEM mode is converted in TE10 whth only a minimum of enegy lost or reflected. Such a transition is a horn.

Note that in order to end with TE mode, walls parallel to the E field are needed, creating other evanescent modes near thir edges. We can consider that the action of the horn is to convert the energy incident into its aperture initially in TEM mode, into another mode suitable to be picked up by a waveguide or cable.

the E/H ratio is same in free space and parallel plates if the matter between the plates is air.

Yes, I agree.

But in free space and in transmission line(air between the plates) the E/H is SAME.

Yes again.

Regards

Z

 

[PlanarMetamaterials]

the E/H ratio is same in free space and parallel plates if the matter between the plates is air.

Yes, I agree.

EDIT: This is correct for TEM modes. Otherwise,

Many electromagnetic texts deal with waveguides, see for example Pozar (3rd Ed.) Chapter 3.2 for PP waveguides, in which equation 3.50 states exactly:

\[{Z}_{TM} = \frac{-{E}_{y}}{{H}_{x}} = \frac{\beta}{\omega\epsilon} = \frac{\beta\eta}{k}\]

Where, from equation 3.45 \[\beta = \sqrt{{k}^{2} - {{k}_{c}}^{2}}\]

In order for \[{Z}_{TM}\] to equal \[\eta\], \[{k}_{c}\] would have to equal 0, i.e., the parallel plates would be have to be infinitely far apart.

The same is for TE modes.

 

[zorro]

Hi PlanarMetamaterials,

look at the posts. We are speaking about TEM mode, not about TE nor TM.
Regards

Z

 

[PlanarMetamaterials]

We are speaking about TEM mode, not about TE nor TM

Yes, you are. That is correct that the E/H ratio is the same in a PPW as free space, but only for TEM modes. I apologize if I didn't make that clear.

That being said, I believe that (someone may wish to correct me on this) for frequencies above kc, the TEM mode is coupled predominantly into a TM mode as it propagates, causing the impedance mismatch.

 

[rodgerwxh]

Try this at your home, find a basin with full water, put a small pipe on the water surface, use your hand to create some waves and try to push the water into the pipe, see if you can successfully put lots of water into the pipe, if you can not, that means those water waves created by your hand do not match the pipe-supported mode. And most of them is reflected. However, you will find a way (angle, direction) that water waves will goes in, in that case, you find the sweet spot or angle to make it work, this is called mode matching. EM field is roughly the same. Only when mode matches, waves goes in, otherwise, reflect.

 

[xuexucheng]

Well. I mentioned a transition needed for the energy transfer between the pair of plates to the load.
Z

Thank you for your excellent reply.
I think if the load resistance is equall to the characteristic impedance of the transmission line, that will be match.

I think this problem is not resolved. We should discuss further.

 

[zorro]

I think if the load resistance is equall to the characteristic impedance of the transmission line, that will be match.

Given that the transmission line composed by two wide plates propagates the mode TEM with the same field configuration that free space, its characteristic impedance should be (with some geometrical scale factor) matched to the intrinsic impedance of free space.
I will check it.

We should discuss further.

OK. To be continued

Z

 

[xuexucheng]

I can not understand the reply.
Could you explain using figure or some other way?
Thank you very much.

The boundary conditions are imposed by the 'boundaries' (i.e. the spatial position of the plates defining the extent) of the transmission line.
For example: visualise two parallel plates of (we'll assume perfectly conductive) metal extending to infinity in the XY plane, spaced (say 1mm) apart such that one plane was at Z = 0 [mm], and the other at Z = 1 [mm]. A TEM wave propagating between the plates is completely invisible to an observer sitting above them at (x=0, y=0, z = 5), for instance. Similarly (by reciprocity), the observer cannot influence the TEM wave travelling between the plates beneath his feet from his position either. (i.e. no transmission/reception/coupling to free space from the transmission line).

Why is this the case? Because the plates are perfectly conductive, there cannot exist any electric field component tangential (i.e. in the same plane) as the plates in the same place they are. If you tried to establish a field gradient parallel to the plate, it would be "shorted out" by the perfect conductor. (Perfect conductor = zero resistance = zero voltage differential irrespective of the induced current). Consequently, only an electric field component *normal* to the plates can exist in their proximity - which gives rise to the only propagating modes between them as the solutions to the wave equation describing the classic TE, TEM and TEM modes. A wave propagating in the free space (where we refer to it being unbounded - i.e. having infinite extent in the case of plane waves, or only loosely constrained in the case of optical Gaussian modes) outside the plates cannot pass through the plates for the same reasons. If the incident wave induces a current in the plate surface as a result of having an electric field component parallel/tangential to the plate, this current causes re-radiation (appearing as a reflection) from the incident surface. Nothing appears on the other side of the plate - it has imposed a "boundary".

I hope that makes some semblance of sense! Unfortunately, most introductions to EM propagation leap straight into a world of div, grad & curl without offering any intuitive insight into the processes going on... sure, it's all there in the vector maths, but I personally couldn't make head or tail of it until I could imagine some physical models to attach it all to - good luck

P.S. What happens if they're *not* perfectly conductive... like copper...? The analysis rapidly gets messy in conductive media and all sorts of interesting effects arise such as the electric field component can now be non-zero at the plate boundary (tiny, sure - but not zero, owing to their finite resistance). This allows an (exponentially decaying) magnitude to exist throughout the metal thickness which gives rise to coupling through the plates etc etc. Lots of fascinating applications! (Underwater comms, for example).

 

[zorro]

Given that the transmission line composed by two wide plates propagates the mode TEM with the same field configuration that free space, its characteristic impedance should be (with some geometrical scale factor) matched to the intrinsic impedance of free space.
I will check it.

Here it is:

Let's consider two long parallel plates of width W and separation D. They form a transmission line, whose characteristic impedance we'll calculate assuming W>>D.
From Ampère's law, the inductance per length l is L=µ₀Dl/W
The capacitance per length is C=ε₀lW/D

Then the characteristic impedance is Z₀=sqrt[(L/l)/(C/l)]=sqrt(µ₀/ε₀)*D/W=η*D/W, where η=377 ohms is the intrinsic impedance of free space.

Imagine that the termination is formed by a resistive sheet, in order to not perturbe the wave propagating along the line. (For this reason it cannot be a lumped resistor.)

Then, the resistivity if the sheet must be η ohms per square (like free space) in order that the termination resistance (with height D and width W) matches the characteristic impedance od the line, Zo.

(Recall that is we have a resistive sheet of ρ ohms per square, a rectangle of length a and width b has a resitance ρa/b. A square would have a resistance ρ, despite the length of its side.)

I hope itis clear. Is it?
Regards

Z