yefj
Advanced Member level 4
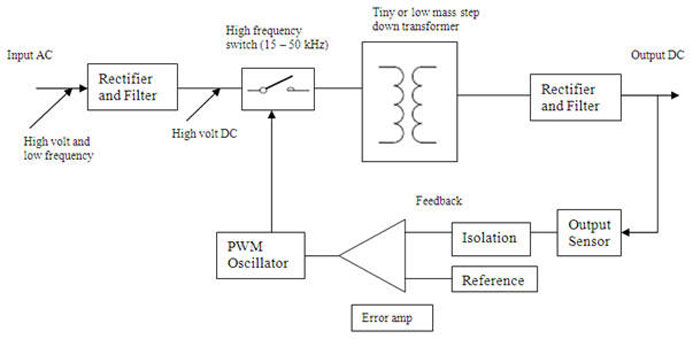
Hello , in the video bellow at 11 minute they say that higher switching frequency the smaller components we can use.
What is the logic that i could understamd why higher switchng frequency allows smaller components?
How can i link the switching frequency to the component size i could use?
Thanks.
What is the logic that i could understamd why higher switchng frequency allows smaller components?
How can i link the switching frequency to the component size i could use?
Thanks.