Vermes
Advanced Member level 4

- Joined
- Aug 2, 2011
- Messages
- 1,163
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,316
- Activity points
- 22,318
This basic mechanism is based on the Ohm's law. It will be described step by step, to make it so obvious for you, that you'll always remember it.
Let's start with the Ohm's law:
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equation that describes this ratio R = V/I.
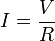
where I is the current through the conductor in units of amperes, V is the potential difference measured across the conductor in units of volts, and R is the resistance of the conductor in units of ohms. More specifically, Ohm's law states that the R in this relation is constant, independent from the current.
Now let's use the Ohm's law:
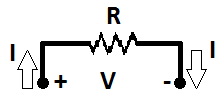
For example if the resistor is 100Ohms and the current is 0.05A, the voltage drop across this resistor will be 5V – this follows from the above formula.
Please take a look for a more appropriate example which is shown below:
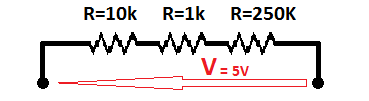
The voltage is 5V and we have 3 resistors. Let's start with counting the current which will flow through this circuit. Basing on the Ohm's law, the current is constant in this circuit.
R=V/I therefore
I=V/R and
I=5[V]/(10kOhms + 1kOhms + 250kOhms)
I=5[V]/261kOhms
I=0.019157088mA
Let's count now the voltage drop across the first resistor:
R=V/I
we need to count V
V=R*I
V=10'000Ohm * 0.019mA
V=0.19157088[V]
Therefore, the voltage drop across this resistor is equal 0.19157[V]
Counting the voltage drop for the second resistor
V=1'000Ohm * 0.019157088mA
V=0.019157088[V]
The voltage drop is equal 0.019157088[V]
And the last voltage drop
U=250'000Ohm * 0.019157088mA
U= 4.789272[V]
The last voltage drop is equal 4.75[V]
Counting the sum: 0.19157088[V] + 0.019157088[V] + 4.789272[V] = 4.999999968[V]
Example 1:
If you want to know where it may be applied, please look at a practical, important example – voltage divider:
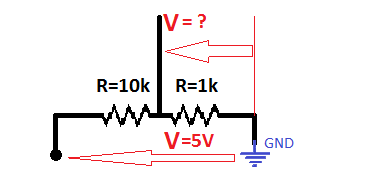
We need to count U, how to do it?
Let's start with counting the current from input to GND:
I=V/R
I=5[V]/(10kOhm + 1kOhm)
I=0.45mA
Now let's count the voltage drop across the second resistor:
V=1'000Ohms * 0.45mA
V=0.45[V]
Therefore, the voltage drop across this resistor is equal 0.45[V]
Let's look now at some equations to count this quicker
input V = 5[V]
input V = I * (R1 + R2) – here 10kOhms and 1kOhm
output V = I * R2
Depending on Ohms equation I = V/R, therefore
(input V)/(R1+R2) = I
(output V)/(R2) = I
substituting into the formula
(input V)/(R1+R2) = (output V)/(R2)
therefore
output V = (input V) * R2/(R1+R2)
If you didn't know how this equation works, I hope that information turned out to be helpful.
Example 2:
Please take a look at another, more complicated example (voltage 5.2V):
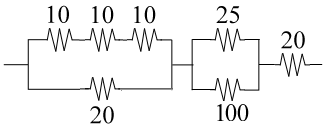
First step:
Count the resistance of each section, lets call them A, B and C.
Section A:
R= 10 + 10 + 10 = 30Ohms
and now
1/R = 1/30 + 1/20
R = 12Ohms
Section B:
1/R = 1/25 + 1/100
R = 20Ohms
Section C:
R= 20Ohms
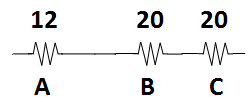
Step two:
Count the total resistance.
R = 52Ohm's
Step three:
Count the total current.
R=V/I
I=V/R
I=5.2[V]/52Ohm's = 0.1A
Step four:
Count voltage drop in each section.
Section A – V= 12Ohm's * 0.1A = 1.2[V]
Section B – V= 20Ohm's * 0.1A = 2.0[V]
Section C – V= 20Ohm's * 0.1A = 2.0[V]
Please always remember to check the calculations 1.2[V] + 2.0[V] + 2.0[V] = 5.2[V]
Step five:
You need to count the current which flows in each net.
Section A up net: I = V/R => I = 1.2[V]/30Ohm's = 0.04A
Section A down net: I = 1.2[V]/20Ohm's = 0.06A
And the voltage drop across resistors.
V = 0.04A * 10Ohm's = 0.4[V]
V = 0.06A * 20Ohm's = 1.2[V]
Count the sum to check the calculation: 3*0.4[V] = 1.2V
Remember that the voltage doesn't split therefore in both nets the voltage should be 1.2V!
Section B:
up net: I=2.0V/25Ohm's = 0.08A
down net: I=2.0V/100Ohm's = 0.02A
And the drops
V = 0.08A * 25Ohm's = 2V
V = 0.02A * 100Ohm's = 2V
Section C is, of course: 2.0V because there is only one resistor
Summary:
OK. That's it, on the end I'll write down the main steps which you need to do to count the voltage drop across resistors:
Let's start with the Ohm's law:
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equation that describes this ratio R = V/I.
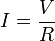
where I is the current through the conductor in units of amperes, V is the potential difference measured across the conductor in units of volts, and R is the resistance of the conductor in units of ohms. More specifically, Ohm's law states that the R in this relation is constant, independent from the current.
Now let's use the Ohm's law:

For example if the resistor is 100Ohms and the current is 0.05A, the voltage drop across this resistor will be 5V – this follows from the above formula.
Please take a look for a more appropriate example which is shown below:

The voltage is 5V and we have 3 resistors. Let's start with counting the current which will flow through this circuit. Basing on the Ohm's law, the current is constant in this circuit.
R=V/I therefore
I=V/R and
I=5[V]/(10kOhms + 1kOhms + 250kOhms)
I=5[V]/261kOhms
I=0.019157088mA
Let's count now the voltage drop across the first resistor:
R=V/I
we need to count V
V=R*I
V=10'000Ohm * 0.019mA
V=0.19157088[V]
Therefore, the voltage drop across this resistor is equal 0.19157[V]
Counting the voltage drop for the second resistor
V=1'000Ohm * 0.019157088mA
V=0.019157088[V]
The voltage drop is equal 0.019157088[V]
And the last voltage drop
U=250'000Ohm * 0.019157088mA
U= 4.789272[V]
The last voltage drop is equal 4.75[V]
Counting the sum: 0.19157088[V] + 0.019157088[V] + 4.789272[V] = 4.999999968[V]
Example 1:
If you want to know where it may be applied, please look at a practical, important example – voltage divider:

We need to count U, how to do it?
Let's start with counting the current from input to GND:
I=V/R
I=5[V]/(10kOhm + 1kOhm)
I=0.45mA
Now let's count the voltage drop across the second resistor:
V=1'000Ohms * 0.45mA
V=0.45[V]
Therefore, the voltage drop across this resistor is equal 0.45[V]
Let's look now at some equations to count this quicker
input V = 5[V]
input V = I * (R1 + R2) – here 10kOhms and 1kOhm
output V = I * R2
Depending on Ohms equation I = V/R, therefore
(input V)/(R1+R2) = I
(output V)/(R2) = I
substituting into the formula
(input V)/(R1+R2) = (output V)/(R2)
therefore
output V = (input V) * R2/(R1+R2)
If you didn't know how this equation works, I hope that information turned out to be helpful.
Example 2:
Please take a look at another, more complicated example (voltage 5.2V):

First step:
Count the resistance of each section, lets call them A, B and C.
Section A:
R= 10 + 10 + 10 = 30Ohms
and now
1/R = 1/30 + 1/20
R = 12Ohms
Section B:
1/R = 1/25 + 1/100
R = 20Ohms
Section C:
R= 20Ohms

Step two:
Count the total resistance.
R = 52Ohm's
Step three:
Count the total current.
R=V/I
I=V/R
I=5.2[V]/52Ohm's = 0.1A
Step four:
Count voltage drop in each section.
Section A – V= 12Ohm's * 0.1A = 1.2[V]
Section B – V= 20Ohm's * 0.1A = 2.0[V]
Section C – V= 20Ohm's * 0.1A = 2.0[V]
Please always remember to check the calculations 1.2[V] + 2.0[V] + 2.0[V] = 5.2[V]
Step five:
You need to count the current which flows in each net.
Section A up net: I = V/R => I = 1.2[V]/30Ohm's = 0.04A
Section A down net: I = 1.2[V]/20Ohm's = 0.06A
And the voltage drop across resistors.
V = 0.04A * 10Ohm's = 0.4[V]
V = 0.06A * 20Ohm's = 1.2[V]
Count the sum to check the calculation: 3*0.4[V] = 1.2V
Remember that the voltage doesn't split therefore in both nets the voltage should be 1.2V!
Section B:
up net: I=2.0V/25Ohm's = 0.08A
down net: I=2.0V/100Ohm's = 0.02A
And the drops
V = 0.08A * 25Ohm's = 2V
V = 0.02A * 100Ohm's = 2V
Section C is, of course: 2.0V because there is only one resistor
Summary:
OK. That's it, on the end I'll write down the main steps which you need to do to count the voltage drop across resistors:
- count the total resistance of the circuit. Sometimes (usually) circuits are more complicated than the viewed earlier. But it is not a problem to count it, just remember that resistance of resistors connected in series sum's and resistors connected in parallel is counted from the below equation:
1/R = 1/Ra + 1/Rb + … + 1/Rz. Please remember that the voltage in parallel nets doesn't divide! - next step is to count the current flow through the circuit (or the voltage, if you know the current). As you know, it is easily counted from Ohm's equation R=V/I
- count the voltage drop across each section
- count the current in each section
- count the voltage drop (using the current counted in the previous step)
